花了数小时阅读了如潮的好评,Bob最终迫不及待为他购买的托斯卡纳全脂牛奶点击了“进行结算”,然后……
哇!刚刚发生了什么?
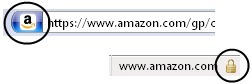
在点击按钮过后的220毫秒时间内,发生了一系列有趣的事情,火狐浏览器(Firefox)不仅改变了地址栏颜色,而且在浏览器的右下角出现了一个小锁头的标志。在我最喜欢的互联网工具Wireshark的帮助下,我们可以通过一个经过略微调整的用于debug的火狐浏览器来探究这一过程。
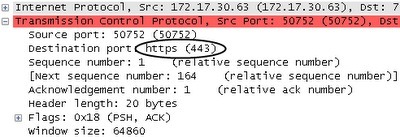
根据RFC 2818标准(译者注:RFC 2818为HTTP Over TLS-网络协议),火狐浏览器自动通过连接的443端口来响应HTTPS请求。
很多人会把HTTPS和网景公司(Netscape)于上世纪九十年代中期创建的SSL(安全套接层)联系起来。事实上,随着时间的推移,这两者之间的关系也慢慢淡化。随着网景公司渐渐的失去市场份额,SSL的维护工作移交给了Internet工程任务组(IETF)。由网景公司发布的第一个版本被重新命名为TLS 1.0(安全传输层协议 1.0),并于1999年1月正式发布。考虑到TLS已经发布了将近10年,如今已经很难再见到真正的SSL通信了。
客户端问候(Client Hello)
TLS将全部的通信以不同方式包裹为“记录”(Records)。我们可以看到,从浏览器发出的第一个字节为0×16(十进制的22),它表示了这是一个“握手”记录。
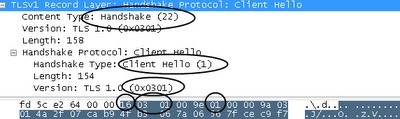
接下来的两个字节是0×0301,它表示了这是一条版本为3.1的记录,同时也向我们表明了TLS1.0实际上是基于SSL3.1构建而来的。
整个握手记录被拆分为数条信息,其中第一条就是我们的客户端问候(Client Hello),即0×01。在客户端问候中,有几个需要着重注意的地方:
随机数:

在客户端问候中,有四个字节以Unix时间格式记录了客户端的协调世界时间(UTC)。协调世界时间是从1970年1月1日开始到当前时刻所经历的秒数。在这个例子中,0x4a2f07ca就是协调世界时间。在他后面有28字节的随机数,在后面的过程中我们会用到这个随机数。
SID(Session ID):

在这里,SID是一个空值(Null)。如果我们在几秒钟之前就登陆过了,我们有可能会恢复之前的会话,从而避免一个完整的握手过程。
密文族(Cipher Suites):
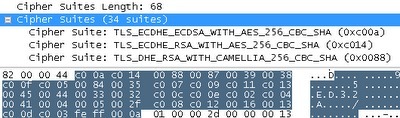
密文族是浏览器所支持的加密算法的清单。整个密文族是由推荐的加密算法“TLS_ECDHE_ECDSA_WITH_AES_256_CBC_SHA”和33种其他加密算法所组成。别担心其他的加密算法会出现问题,我们一会儿就会发现Amazon也没有使用推荐的加密算法。
Server_name扩展:

通过这种方式,我们能够告诉:浏览器正在试图访问https://。这确实方便了很多,因为我们的TLS握手时间发生在HTTP通信之前,而HTTP请求会包含一个“Host头”,从而使那些为了节约成本而将数百个网站域名解析到一个IP地址上的网络托管商能够分辨出一个网络请求对应的是哪个网站。传统意义上的SSL同样要求一个网站请求对应一个IP地址,但是Server_name扩展则允许服务器对浏览器的请求授予相对应的证书。如果没有其他的请求,Server_name扩展应该允许浏览器访问这个IPV4地址一周左右的时间。
服务器问候(Server Hello)
回复的握手记录由两个比较大的包组成(2551字节)。记录中包含了0×0301的版本信息,意味着Amazon同意我们使用TLS1.0访问的请求。这条记录包含了三条有趣的子信息:
1.服务器问候信息(Server Hello)(2):
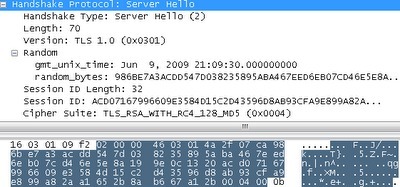
我们得到了服务器的以Unix时间格式记录的UTC和28字节的随机数。
32字节的SID,在我们想要重新连接到的时候可以避免一整套握手过程。
在我们所提供的34个加密族中,Amazon挑选了“TLS_RSA_WITH_RC4_128_MD5”(0×0004)。这就意味着Amazon会使用RSA公钥加密算法来区分证书签名和交换密钥,通过RC4加密算法来加密数据,利用Md5来校验信息。我们之后会深入的研究这一部分内容。我个人认为,Amazon选择这一密码组是有其自身的原因的。在我们所提供的密码族中,这一加密组的加密方式是CPU占用最低的,这就允许Amazon的每台服务器接受更多的连接。当然了,也许还有一个原因是,Amazon是在向这三种加密算法的发明者Ron Rivest(罗恩·李·维斯特)致敬。
2.证书信息(11):
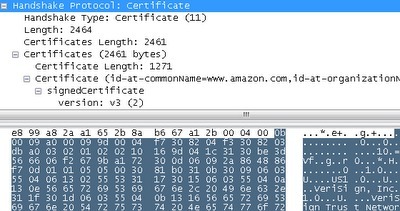
这段巨大的信息共有2464字节,其证书允许客户端在Amazon服务器上进行认证。这个证书其实并没有什么奇特之处,你能通过浏览器浏览它的大部分内容。
3.服务器问候结束信息(14):

这是一个零字节信息,用于告诉客户端整个“问候”过程已经结束,并且表明服务器不会再向客户端询问证书。
校验证书
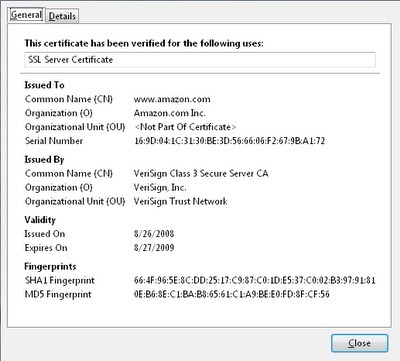
此时,浏览器已经知道是否应该信任。在这个例子中,浏览器通过证书确认网站是否受信,它会检查 的证书,并且确认当前的时间是在“最早时间”2008年8月26日之后,在“最晚时间”2009年8月27日之前。浏览器还会确认证书所携带的公共密钥已被授权用于交换密钥。
为什么我们要信任这个证书?
证书中所包含的签名是一串非常长的大端格式的数字:

任何人都可以向我们发送这些字节,但我们为什么要信任这个签名?为了解释这个问题,我们首先要回顾一些重要的数学知识:
RSA加密算法的基础介绍
人人常常会问,编程和数学之间有什么联系?证书就为数学在编程领域的应用提供了一个实际的例子。Amazon的服务器告诉我们需要使用RSA算法来校验证书签名。什么又是RSA算法呢?RSA算法是由麻省理工(MIT)的Ron Rivest、Adi Shamirh和Len Adleman(RSA命名各取了三人名字中的首字母)三人于上世纪70年代创建的。三位天才的学者结合了2000多年数学史上的精华,发明了这种简洁高效的算法:
选取两个较大的初值p和q,相乘得n;n = p*q 接下来选取一个较小的数作为加密指数e,d作为解密指数是e的倒数。在加密的过程中,n和e是公开信息,解密密钥d则是最高机密。至于p和q,你可以将他们公开,也可以作为机密保管。但是一定要记住,e和d是互为倒数的两个数。
假设你现在有一段信息M(转换成数字),将其加密只需要进行运算:C ≡ Me (mod n)
这个公式表示M的e次幂,mod n表示除以n取余数。当这段密文的接受者知道解密指数d的时候就可以将密文进行还原:Cd ≡ (Me)d ≡ Me*d ≡ M1 ≡ M (mod n)
有趣的是,解密指数d的持有者还可以将信息M进行用解密指数d进行加密:Md ≡ S (mod n)
加密者将S、M、e、n公开之后,任何人都可以获得这段信息的原文:Se ≡ (Md)e ≡ Md*e ≡ Me*d ≡ M1 ≡ M (mod n)
如同RSA的公共密钥加密算法经常被称之为非对称算法,因为加密密钥(在我们的例子中为e)和解密密钥(在我们的例子中是d)并不对称。取余运算的过程也不像我们平常接触的运算(诸如对数运算)那样简单。RSA加密算法的神奇之处在于你可以非常快速的进行数据的加密运算,即 ,但是如果没有解密密码d,你将很难破解出密码,即运算 将不可能实现。正如我们所看到的,通过对n进行因式分解而得到p和q,再推断出解密密钥d的过程难于上青天。
签名验证
在使用RSA加密算法的时候,最重要的一条就是要确保任何涉及到的数字都要足够复杂才能保证不被现有的计算方法所破解。这些数字要多复杂呢?的服务器是利用“VeriSign Class 3 Secure Server CA”来对证书进行签名的。从证书中,我们可以看到这个VeriSign(电子签名校验器,也称威瑞信公司)的系数n有2048位二进制数构成,换算成十进制足足有617位数字:
1890572922 9464742433 9498401781 6528521078 8629616064 3051642608 4317020197 7241822595 6075980039 8371048211 4887504542 4200635317 0422636532 2091550579 0341204005 1169453804 7325464426 0479594122 4167270607 6731441028 3698615569 9947933786 3789783838 5829991518 1037601365 0218058341 7944190228 0926880299 3425241541 4300090021 1055372661 2125414429 9349272172 5333752665 6605550620 5558450610 3253786958 8361121949 2417723618 5199653627 5260212221 0847786057 9342235500 9443918198 9038906234 1550747726 8041766919 1500918876 1961879460 3091993360 6376719337 6644159792 1249204891 7079005527 7689341573 9395596650 5484628101 0469658502 1566385762 0175231997 6268718746 7514321
(如果你想要对这一大串数字进行分解因式获得p和q,那就祝你好运!顺便一提,如果你真的计算出了p和q,那你就破解了数字签名证书了!)
这个VeriSign的加密密钥e是 。当然,他们将解密密钥d保管得十分严密,通常是在拥有视网膜扫描和荷枪实弹的警卫守护的机房当中。在签名之前,VeriSign会根据相关约定的技术文档,对证书上所提供的信息进行校验。一旦证书信息符合相关要求,VeriSign会利用SHA-1哈希算法获取证书的哈希值(hash),并对其进行声明。在Wireshark中,完整的证书信息会显示在“signedCertificate”(已签名证书)中:
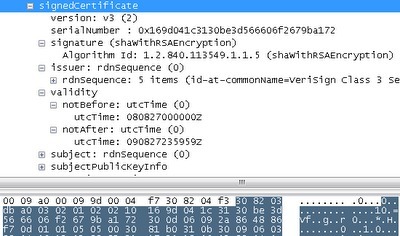
这里应该是软件的用词不当,因为这一段实际上是指那些即将被签名的信息,而不是指那些已经包含了签名的信息。
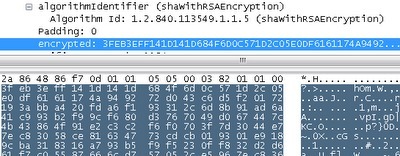
实际上经过签名的信息S,在Wireshark中被称之为“encrypted”(密文)。我们将S的e次幂除以n取余数(即公式: )就能计算出被加密的原文,其十六进制如下:
0001FFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFFFFFFFFFF FFFFFFFF00302130 0906052B0E03021A05000414C19F8786 871775C60EFE0542 E4C2167C830539DB
根据PKCS#1 v1.5标准(译者注:The Public-Key Cryptography Standards (PKCS)是由美国RSA数据安全公司及其合作伙伴制定的一组公钥密码学标准)规定:“第一个字节是00,这样就可以保证加密块在被转换为整数的时候比其加密参数要小。”第二个字节为01,表示了这是一个私有密钥操作(数字签名就是私有密钥操作的一种)。后面紧接着的一连串的FF字节是为了填充数据,使得这一串数字变得足够大(加大黑客恶意破解的难度)。填充数字以一个00字节结束。紧接着的30 21 30 09 06 05 2B 0E 03 02 1A 05 00 04 14这些字节是PKCS#1 v2.1标准中用于说明这段哈希值是通过SHA-1算法计算而出的。最后的20字节是SHA-1算法所计算出来的哈希值,即对未加密信息的摘要描述。(译者注:原文中这里使用了带引号的signedCertificate,根据作者前文描述,这应该是Wireshark软件的bug,实际上应指的是未被加密的信息。)
因为这段信息的格式正确,且最后的哈希值与我们独立计算出来的校验一致,所以我们可以断定,这一定是知道“VeriSign Class 3 Secure Server CA”的解密密钥d的人对它进行了签名。而世界上只有VeriSign公司才知道这串密钥。
当然了,我们也可以重复验证这个“VeriSign Class 3 Secure Server CA”的证书的确是通过VeriSign公司的“第三类公私证书认证(Class 3 Public Primary Certification Authority)”进行签名的。
但是,即便是这样,我们为什么要信任VeriSign公司?整个的信任链条就此断掉了。
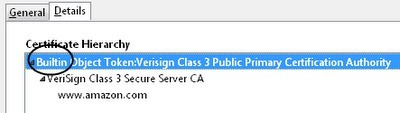
由图可以看到,“VeriSign Class 3 Secure Server CA”对进行了签名,而“VeriSign Class 3 Public Primary Certification Authority”对“VeriSign Class 3 Secure Server CA”进行了签名,但是最顶部的“VeriSign Class 3 Public Primary Certification Authority”则对自己进行了签名。这是因为,这个证书自从NSS(网络安全服务)库中的certdata.txt 升级到1.4版之后就作为“受信任的根证书颁发机构”(译者注:参照微软官方翻译)被编译到了Mozilla产品中(火狐浏览器)。这段信息是由网景公司的Robert Relyea于2000年9月6日提交的,并随附以下注释:
“由仅存的NSS编译了框架。包含一个在线的certdata.txt文档,其中包含了我们受信的跟证书颁发机构(一旦我们获得了其他受信机构的许可会陆续将他们添加进去)”。
这个举动有着相当长远的影响,因为这些证书的有效日期是从1996年1月28日到2028年1月1日。
肯·汤普逊(Ken Thompson)在他的《对深信不疑的信任》(译者注:Reflections on Trusting Trust是肯汤普逊1983年获得图灵奖时的演说)的演说中解释的很好:你最终还是要绝对信任某一人,在这个问题上没有第二条路可走。在本文的例子中,我们就毫无保留的信任Robert Relyea做了一个正确的决定。我们同样希望Mozilla在自己软件中加入“受信任根证书颁发机构”这种行为也是合理的吧。
这里需要注意的是:这一系列的证书和签名只是用来形成一个信任链。在公共互联网上,VeriSign的根证书被火狐浏览器完全信任的时间远早于你接触互联网。在一个公司中,你可以创建自己的受信任的根证书颁发机构并把它安装到任何人的计算机中。
相对的,你也可以购买VeriSign公司的业务,降低整个证书信任链的信任风险。通过第三方的认证机构(在这个例子里是VeriSign公司)我们能利用证书建立起信任关系。如果你有类似于“悄悄话”的安全途径来传递一个秘密的key,那你也可以使用一个预共享密钥(PSK)来建立起信任关系。诸如TLS-PSK、或者带有安全远程密码(SRP)的TLS扩展包都能让我们使用预共享密钥。不行的是,这些扩展包在应用和支持方面远远比不上TLS,所以他们有的时候并不实用。另外,这些替代选项需要额外德尔安全途径进行保密信息的传输,这一部分的开销远比我们现在正在应用的TLS庞大。换句话说,这也就是我们为什么不应用那些其他途径构建信任关系的原因。
言归正传,我们所需要的最后确认的信息就是在证书上的主机名跟我们预想的是一样的。Nelson Bolyard在SSL_AuthCertificate 函数中的注释为我们解释其中的原因:
“SSL连接的客户端确认证书正确,并检查证书中所对应的主机名是否正确,因为这是我们应对中间人攻击的唯一方式!” (译者注:中间人攻击是一种“间接”的入侵攻击,这种攻击模式是通过各种技术手段将受入侵者控制的一台计算机虚拟放置在网络连接中的两台通信计算机之间,这台计算机就称为“中间人”。)
/* cert is OK. This is the client side of an SSL connection.
* Now check the name field in the cert against the desired hostname.
* NB: This is our only defense against Man-In-The-Middle (MITM) attacks! */
这样的检查是为了防止中间人攻击:因为我们对整个信任链条上的人都采取了完全信任的态度,认为他们并不会进行黑客行为,就像我们的证书中所声称它是来自,但是假如他的真实来源并非,那我们可能就有被攻击的危险。如果攻击者使用域名污染(DNS cache poisoning)等技术对你的DNS服务器进行篡改,那么你也许会把黑客的网站误认为是一个安全的受信网站(诸如),因为地址栏显示的信息一切正常。这最后一步对证书颁发机构的检查就是为了防止这样的事情发生。
随机密码串(Pre-Master Secret)
现在我们已经了解了的各项要求,并且知道了公共解密密钥e和参数n。在通信过程中的任何一方也都知道了这些信息(佐证就是我们通过Wireshark获得了这些信息)。现在我们所需要做的事情就是生成一串窃密者/攻击者都不能知道的随机密码。这并不像听上去的那么简单。早在1996年,研究人员就发现了网景浏览器1.1的伪随机数发生器仅仅利用了三个参数:当天的时间,进程ID和父进程ID。正如研究人员所指出的问题:这些用于生成随机数的参数并不具有随机性,而且他们相对来说比较容易被破解。
因为一切都是来源于这三个随机数参数,所以在1996,利用当时的机器仅需要25秒钟的时间就可以破解一个SSL通信。找到一种生成真正随机数的方法是非常困难的,如果你不相信这一点,那就去问问Debian OpenSSL的维护工程师吧。如果随机数的生成方式遭到破解,那么建立在这之上的一系列安全措施都是毫无意义的。
在Windows操作系统中,用于加密目的随机数都是利用一个叫做CryptGenRandom的函数生成的。这个函数的哈希表位对超过125个来源的数据进行抽样!火狐浏览器利用CryptGenRandom函数和它自身的函数来构成它自己的伪随机数发生器。(译者注:之所以称之为伪随机数是因为真正意义上的随机数算法并不存在,这些函数还是利用大量的时变、量变参数来通过复杂的运算生成相对意义上的随机数,但是这些数之间还是存在统计学规律的,只是想要找到生成随机数的过程并不那么容易)。
我们并不会直接利用生成的这48字节的随机密码串,但是由于很多重要的信息都是由他计算而来的,所以对随机密码串的保密就显得格外重要。正如我之前所预料到的,火狐浏览器对随机密码串的保密十分严格,所以我不得不编译了一个用于debug的版本。为了观察随机密码串,我还特地设置了SSLDEBUGFILE和SSLTRACE两个环境变量。
其中,SSLDEBUGFILE显示的就是随机密码串的值:
1


