设计中的手绘几何图案作图法之基础理论篇

在早期文明时期，科学(主要是数学)、宗教和艺术是没有分开的。我们甚至很难找个名词去解释这个“杂烩”式的学科，也很难想象这三个领域的贯通之处。但只要看看那些几何感设计的伟大作品，尤其是那些巨作的片段所透露出的信息，你就会感到这三者的确相互联系、共同存在。

几何图形就是视觉化的数学，很久以来它都是由一些诸如1、2、3这样简单的数字所构建。早期的几何学家只需要经过肉眼观察图形本身，就可以了解几何图形之间是如何联系，并理解它们在数字层面的联系。每一种图案都隐含着数字里的深意。这些二维的、抽象的几何图案是作为靠近空性和未知神域、超越我们的现实世界的一步。它的美的确是超凡脱俗的。

对几何以及数字图案的沉迷在今天又一次发生了：从不断发展的分形艺术中就能看出端倪。完全没有用到任何专门软件去创造一个非常复杂的几何图形，事实上它本身就已经足够，且能带给你更多的思考。你可以从一张空无的白纸上慢慢画出几何图案，这也就是我们的教程所要教给你的，尽管已经有那么多的软件，但人类依然离不开手绘。

术语

在教程开始的时候，我将和大家一起定义一组术语。在接下来的时间里，我们会常常遇到这些术语。你们大部分人相信应该也对它们非常熟悉了。

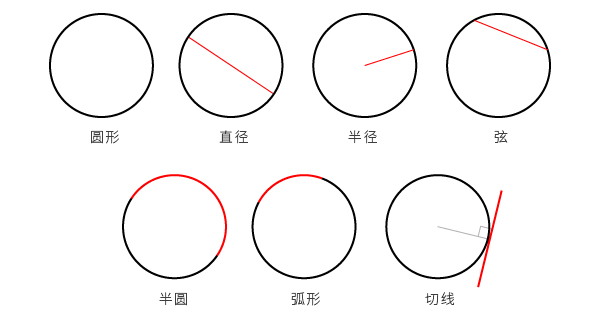
圆形：这是最简单的几何图形，在一个封闭的曲线内所有点到圆点的距离都相等。

直径：任何一条连接圆形上两点、并且还能同时穿过圆点的线段。

半径：任何一条从圆形上任意点连接圆心的线段。(圆规就是利用半径来画圆的)

弦：任何一条连接圆形上两点、并且不经过圆心的线段。

半圆：圆形的一半。

弧形：圆形上除了半圆的任何一个片段。

切线：一条线刚刚接触到圆形中的单个点。

锐角：小于90度的角。

直角：等于90度的角。通常我们用一个小正方形标记直角，如上图所示。

钝角：大于90度的角。

三角形：三条直线组成的封闭图形。与下面三类三角形不同的是不等边三角形。任一三角形内三个角的度数之和都是180度。

直角三角形：其中一个角是直角的三角形。另外的两个角不一定相等，它的边长会有变化。

等腰三角形：两条边长相等的三角形。

等边三角形：三条边长相等的三角形，它的三个角都相等且都等于60度。

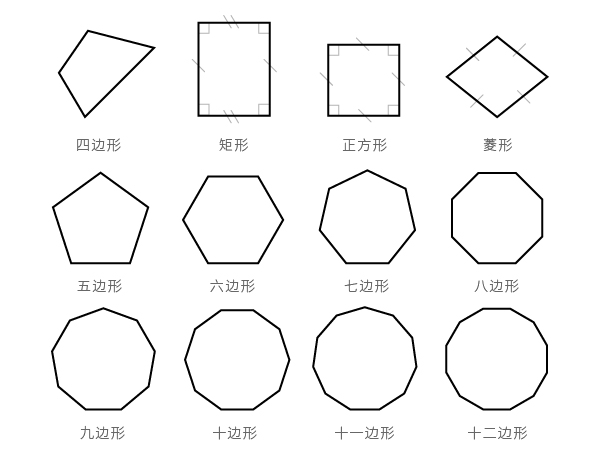
四边形：由四条直线组成的封闭图形。在一个四边形内四个角的度数之和为360度。

矩形：四个角都是直角的四边形。同时，矩形的四条边长两两平行且等长。

正方形：这是一个特殊的矩形，它的四条边边长长度都相等。

菱形:四条边等长，相对的边平行，但是没有直角。

接下来八个图形统称为多边形(大于四条边的封边图形)，从五、六直到十二条边。每个图形内的边长等长，角的度数相等。

工具

最初的几何工具就是一些绳子和钉子，的确也不是什么厉害的工具，只是在当时来看已经足够精确。而当纸张深入人类的生活，你需要的工具就是这三样：一支铅笔、一把直尺、一个圆规。

铅笔

一支铅笔就能画出图形，这大家都十分清楚，但千万别抓到一支铅笔就马上开始画了，你得找到适合硬度的铅笔才行。在下图中你会看到橙色铅笔上标注的HB，灰色的铅笔上标注的是6H.这就是说明铅笔的硬度。B是值的柔软度，B的数字越大(如4B、5B)，就越柔软。

柔软的笔芯会留下较黑的笔迹，它也相对不会划伤画纸，但也很容易被弄脏。H指的是笔芯的硬度，它同样被分级，它的笔迹相对较细较浅，也不会容易弄脏，但是，如果你使用HB的笔用力在纸上划一划，就能使硬度和柔软度都达到平衡。

当你开始为几何图案最初造型时，请放弃使用软头铅笔!道理很简单，所构建的黑色线条很快就会看上去模糊不清，弄脏是在所难免。软头笔芯的笔尖也很快就会变钝，在画画的时候会让你重复削尖它好几次。

在图案造型时，你要使用较细浅的线条来勾勒，当一旦定型后，你就可以用软而黑的画笔来描出最终的图案。这也是这两种铅笔存在的原因：6H可以长久保持尖锐，画出最细的线，而最终的图案由HB来勾勒。

在非常复杂的图案里，可能需要画一些略黑一些的细线，这时你可以选择诸如3H或者2H的笔芯。这非常重要，学会轻轻握住H铅笔去画，因为他们确实是很容易伤到纸的表面，而且也不易擦除。当你用铅笔描绘完毕后，图案还可以用钢笔勾勒一次，这时，铅笔的部分就能被轻松地擦除或者会被钢笔覆盖。如果你愿意，还能通过临摹而将图案转移到一张新的干净的图纸上。

传统的铅笔的好处是它们较坚韧，笔芯不容易折断，但它的缺点就在于你需要根据绘图的实际情况，不停用小刀削尖它们。我个人推荐的替代方案是采用这种好用的2mm的自动铅笔，就像我下图里展示的这支，以及非常特殊的削笔刀和替换笔芯。你可以买一支这样的铅笔，在需要的时候还能随时替换笔芯。不要买那种太细的笔芯，如0.5mm，因为它们的笔尖已经不可能再细了，而且这种笔是没有硬度和柔软度的分别的。

直尺或普通尺子

严格来说，在几何学是决不能使用测量的，因为几何图案与实际造型不同，在本系列课程中你也绝不会用到测量。

作为精准的工具，你得选那些专业的为建筑业提供产品的品牌。你会觉得奇怪，难道其他品牌做的尺子就不够好吗?答案是：当然不够!刻度也许无关紧要，但是它的笔直却是非常重要的!

这有个诀窍来测量尺子的直边：沿着尺子的边画一条线，然后围绕尺子的这条边将尺子翻转，沿着同一条边，在刚刚那条边的上方再画上相同的线(这里看是否两条线能完全重合)。我很久开始，就用这个方式测试真正的货真价实的直尺。

让我们拉近距离观察：看看刚刚画的两条线是否能完全重合成为一条线?这就意味着尺子的边是否笔直。

接下来，我用钢尺来测试，你会看到为什么钢尺只能用来裁纸，用做精准工作时就不大适合

在上图的特写中，你是否可以看到一条线朝右边时已经逐渐开始分开?如果整个直线能撑大到整个电脑屏幕的话，你将会看见即便这两条线是沿着同一条边画下的，他们之间还有个非常细密的空间，这意味着这条边稍微歪斜，这也是我们在尽量避免的。

圆规

我们所用的最有意思和最重要的工具，也是最昂贵的工具，无疑是圆规啦!一个好的圆规是值回票价的，它的金属外形也十分耐用。你也可以用那种学生圆规，当然，等到你进阶以后再买一把真正的专业圆规(否则你会因为其精确性而抓狂)。

一个基本的圆规是由两条腿与连接它们的铰链所组成的：一条腿是一个针尖，另一条腿是铅笔的笔尖。铅笔那条腿可以自由开合，针尖的腿可以固定于纸面，铅笔就能围绕它旋转，旋转一周就画上一个圆。你可以完全就单单用圆规画出一个复杂的几何图案。这与远古时期的用绳子和钉子来画图也异曲同工了。

关于圆规的功能说明

1、通过扭紧螺丝来调整圆规的开合度。如果你不调紧它，那么在工作中，画圆的半径大小就不可避免会被随意改变。

2、一个可替换的铅笔笔尖。上图中圆规的右边脚的笔尖利用右边的那个小装置就能替换，这在任何绘图工具中都能插入诸如铅笔、钢笔、绘图笔，甚至是直尺。这真的是非常好用，再也不会出现徒手画出的墨水或其他颜色的线条来打破整个绘图的完美构造了。

3、可延伸性：在底部有一个让圆规腿变得更长的装置。这让你可以画上更大的圆。例如，这个圆规最大只能画半径为25cm的圆，但是延伸的腿就能让这个极限达到35cm。

有些圆规是没有笔芯的，但它是专为配合铅笔使用而设计的。这很好，这完全取决于个人喜好了。对于支持或反对这类圆规的人，我的解释都是这样：这类似于当你使用传统铅笔和自动铅笔一样，需要自己来斟酌。

使用圆规的诀窍

画圆时最好用一张厚的卡片固定于你的作品表面，以免圆规针尖刺伤到作品，同时，你也要确保这张卡片也能固定，否则，这个过程就很容易失控。

使用时用大拇指和食指握住顶端的把手，旋转它就能创建出一个圆。一开始很常见的现象是，你需要经过练习才能画出一个完美的圆。在画圆时，尽量保持圆规的针尖垂直于纸面。就算是调整圆规大小的时候，也不要只握住圆规的一条腿。

我必须强调的还有一点：保持针尖锋利，同时也要确保笔芯也是尖锐的。这就是有的人画几何图形很在行而有的就是画不好的原因。

设计中的手绘几何图案作图法之实战篇

好了，基础理论已经掌握后，让我们开始动手，拿出纸和绘图工具来吧!

图示说明

我们通篇的教程会出现构图时的一些图示说明如下：

三角形（给定一条边）

如果要在给定的一条直线画出一个三角形，这就意味着你已经画好了一条边了。

步骤1：

利用圆规，以A点为圆心，AB线为半径，画上一个弧形。

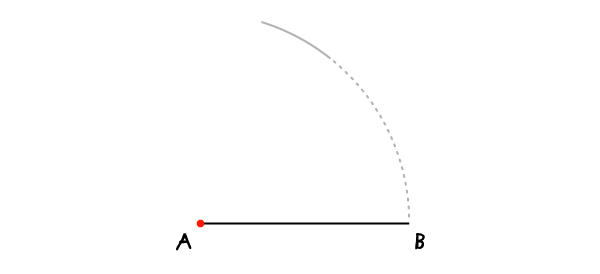
步骤2：

利用圆规，以B点为圆心，AB线为半径，画上另一条弧形，这条弧形与上一条弧形交于C点。

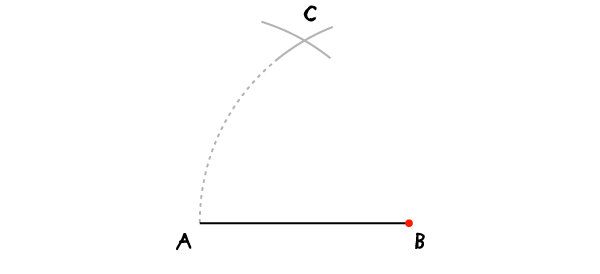
步骤3：

连接AB两点到C点，形成一个等边三角形。如果你圆规半径大小大于或小于AB线段的长度，那么这个三角形就不是一个等边三角形，而是等腰三角形。

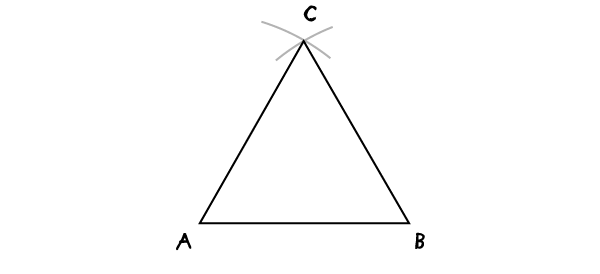
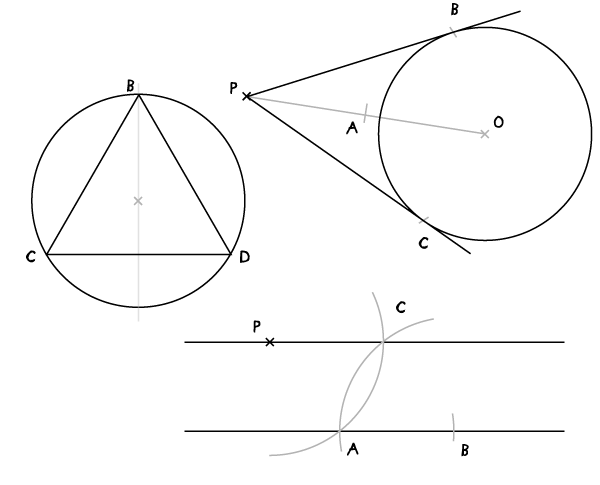
三角形（在一个圆内）

如果已经给定了一个圆，需要在这个圆内画三角形，这个三角形要内切这个圆且为等长三角形(这意味着三角形的三个点都在这个圆上)，按照如下步骤画：

步骤1:

穿过圆心画一条线，与圆相交于A、B两点。

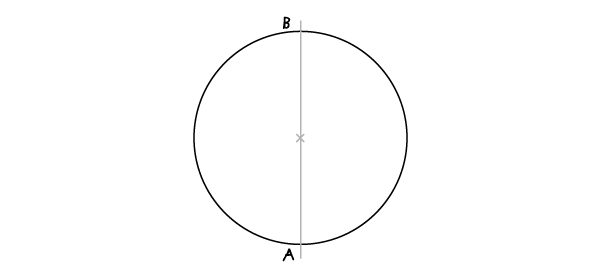
步骤2：

圆规半径与这个圆相同，将圆心固定于A点，画上一条弧线，弧线与圆交于C、D两点。

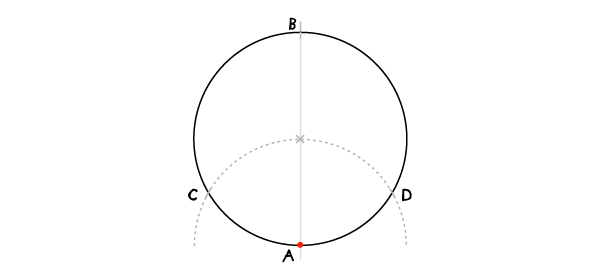
步骤3：

连接ACD三个点

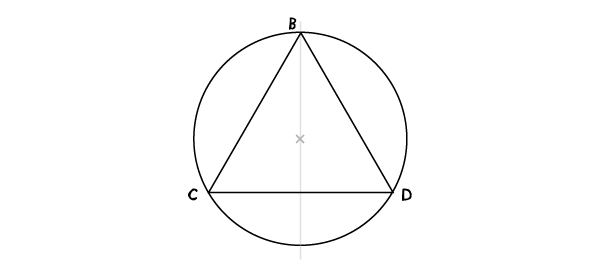
垂直平分线

这个听起来很有技术含量的名词提及到一条具有两个属性的线：这条线(或这个角)被平均分为了两部分(或被平均分为了两个角);按照这个中点延长成为一条线，刚好与原线构成直角。这是一个非常重要的方法，在构造其他图形时会频繁使用到。

步骤1：

以A点为圆心，圆规半径为AB，画上一条弧线。

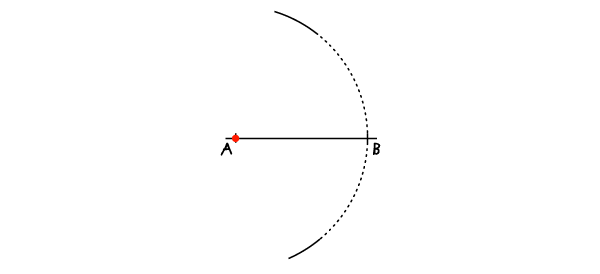
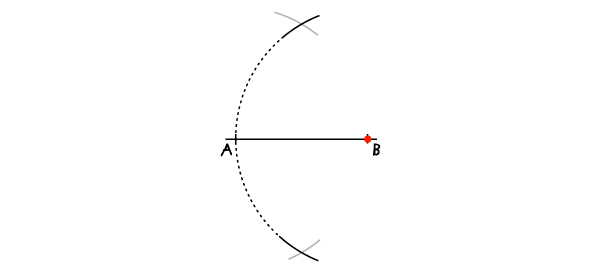
步骤2：

以B点为圆心，AB为半径，画上另一条弧线。两条弧线相交两点如下：

步骤3：

连接相交的两点。这条连接线刚好将AB对半分成两段，它们相交于O点，刚好是AB的中点，并且相互垂直。

一个圆上给定点的切线

如果在一个圆上给定了一点(P点)，要穿过这个点画一条切线应该怎么画?

步骤1：

经过P点画一条经过圆心O的半径，将半径延长与圆相交于A点。

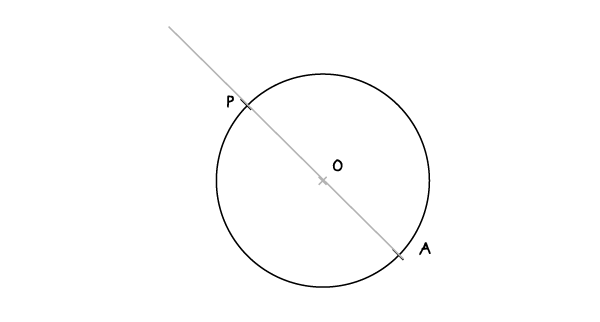
步骤2：

将圆规半径大小调整为AP，将圆心固定于O点，画一个较大的弧形，弧形的跨度相当于一个半圆。AP的延长线交这个弧形与B点。

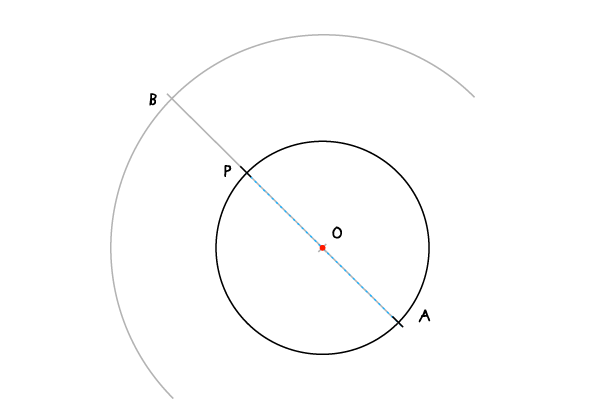
步骤3：

不改变圆规的半径，将圆心固定于B点，画一条弧线，这条弧形交上一步骤所画弧线于C、D点。

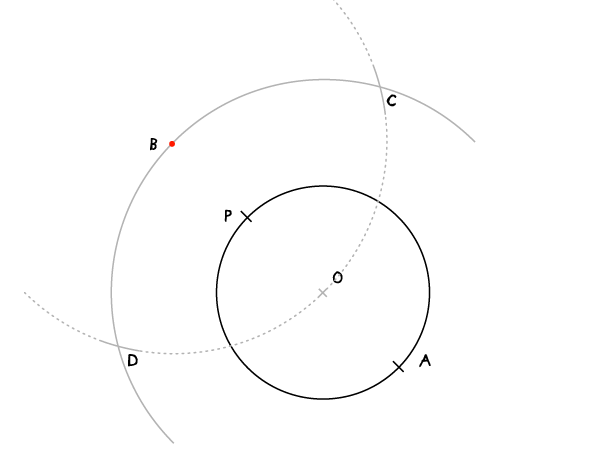
步骤4:

连接CD点，就是P点的在这个圆的正切线。

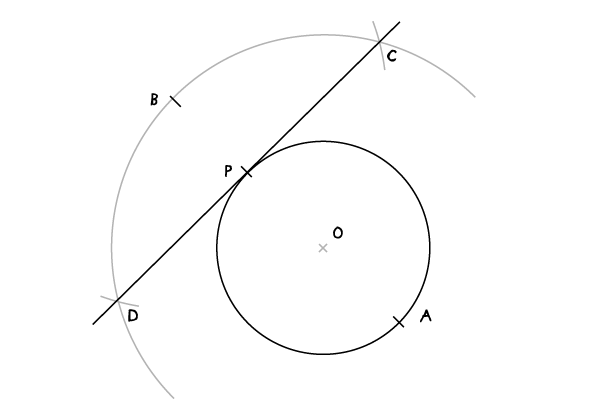
圆外一点的切线

假设P点是圆外的一点，你需要经过P点画这个圆的切线，怎么画?

步骤1：

连接圆心O点和P点。

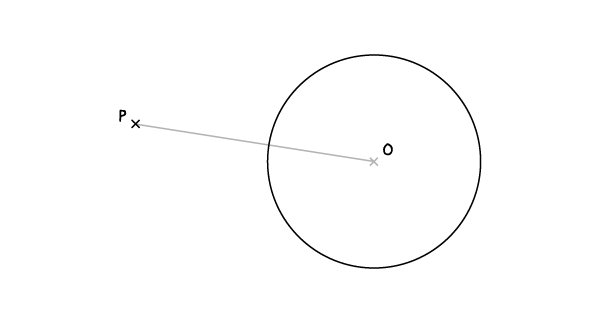
步骤2：

将PO线对半分于A点。

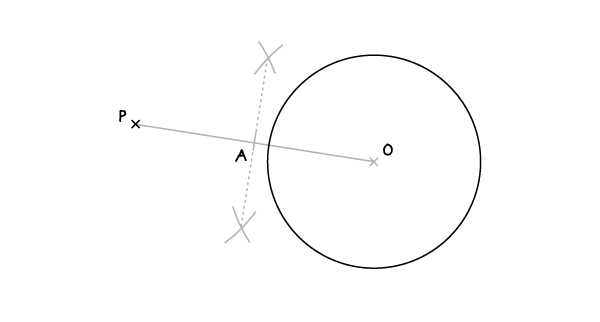
步骤3：

将圆心固定于A点，AO为半径画一条弧线，这条弧线交圆于B、C两点。

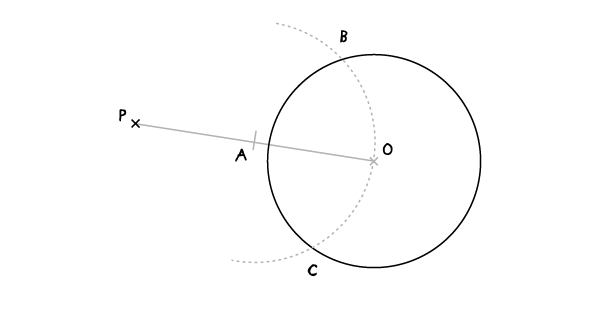
步骤4：

PB和PC就是经过P点的切线。

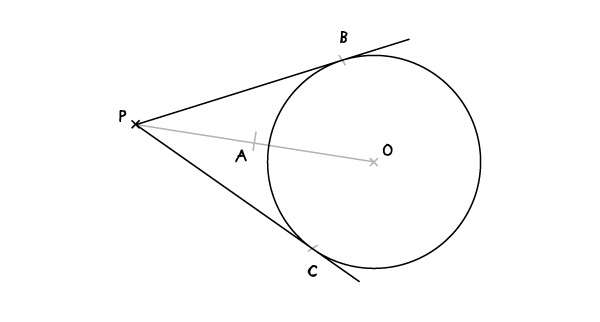
平行线（经过给定的一个点）

平行线就是两条永不相交的线，所以它们的方向永远保持一致。很多人已经在学校时就学过用两把直尺来画平行线，今天我们来用一个新方法来画平行线。

让我们从给定一条线开始，假设已经给定了一点P点，需要另一条线从这点穿过。

步骤1：

P点作为圆心，画上一条弧线交这条线于A点。

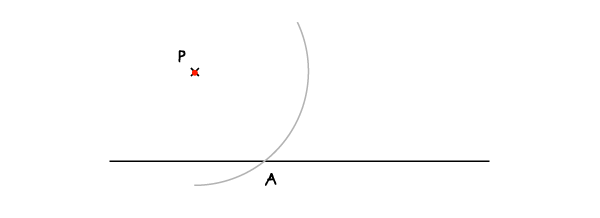
步骤2：

保持同样大小半径，将圆心固定于A点画一条弧线交这条线于B点。

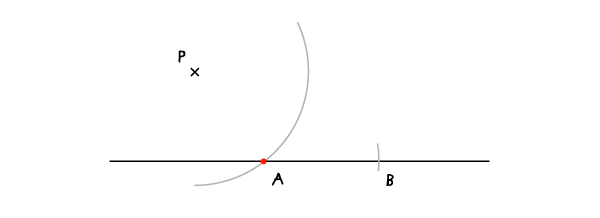
步骤3：

将圆心固定于B点，AB为半径画一条弧线，这条弧形与步骤1所画弧线交于C点。

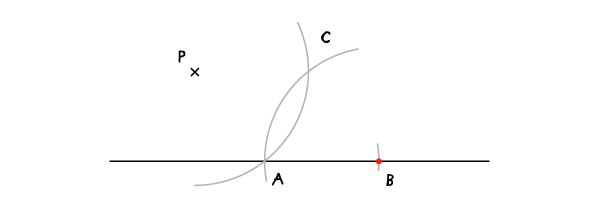
步骤4：

连接PC线就是AB线的平行线。

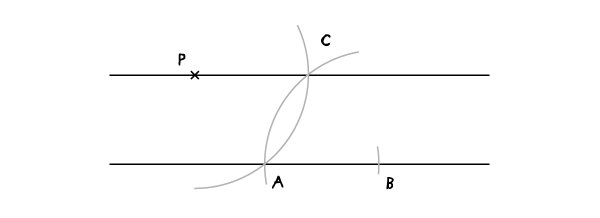
平行线（自己来选定平行线距离）

下面要教的是，要画一组平行线，平行线之间的距离可以自己来选定，应该怎么画呢?

步骤1：

在这条线上画上两对点，也就是出现有AB和CD两条线段，线段间的距离不确定，但这两对线段离得越远，结果就越精确。

步骤2:

为两条线段分别画上中线(也即是用一条线将线段平分为二)

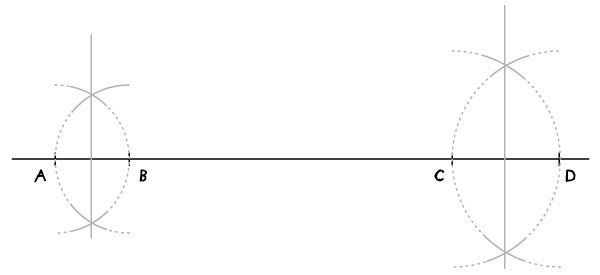
步骤3：

打开你的圆规，选择你想要的平行距离，也即是圆规的半径。将圆心固定于两条线段的中点，画上两条弧线。两条弧线分别交中线于一点。

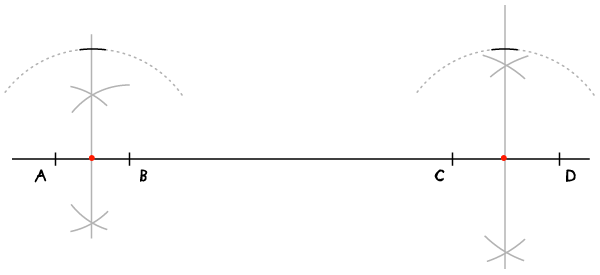
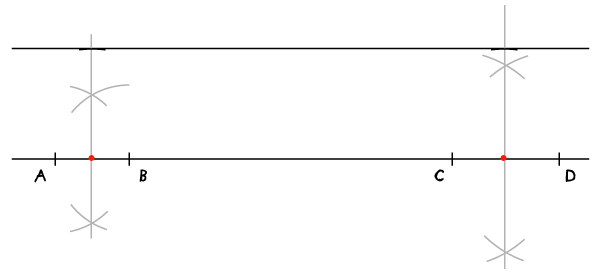
步骤4：

连接这两点。

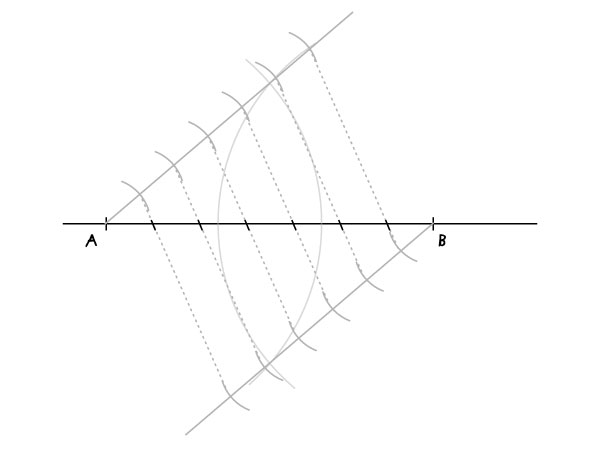
将线段等分

我们想要划分一条线段成为几等分的时候应该怎么做?这里我教大家一个妙招。如果你的手边没有可以度量的尺子，即使你有，你也很难度量出诸如5.63cm这样精确的长度。这个方法非常精确，它也需要一些计算的能力。

如下例所示，我们现在想将这条线段平均分为七等分。

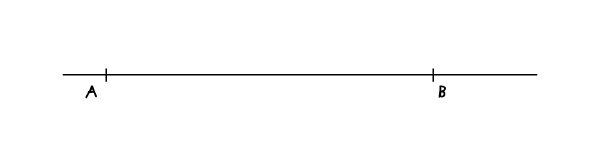
步骤1：

将圆心分别固定于A、B两点，画上两条相对的弧线。这里的半径随意，只要能让它们相交即可。

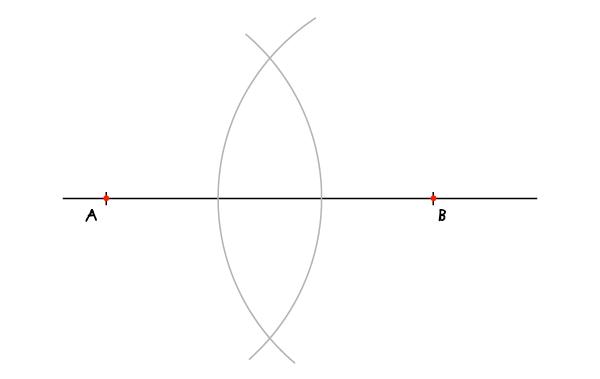
步骤2：

连接A点到其中一个交点，B点到另一个交点，这样两条线是相互平行的。

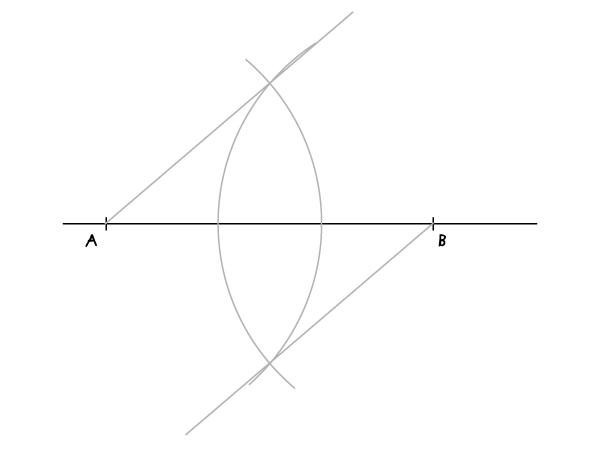
步骤3：

我们现在要做的就是利用圆规，将两条平行线分别进行标记。半径大小并不重要，只要保持小一点让所有点都能适应这条线就OK。画上一条弧形后，让这条弧形交于平行线上的一点就是一个标记。这里要标记的数量是，比如本例中我们要划分七等分，那么标记数量就是6个。下面是我作的第一个标记。

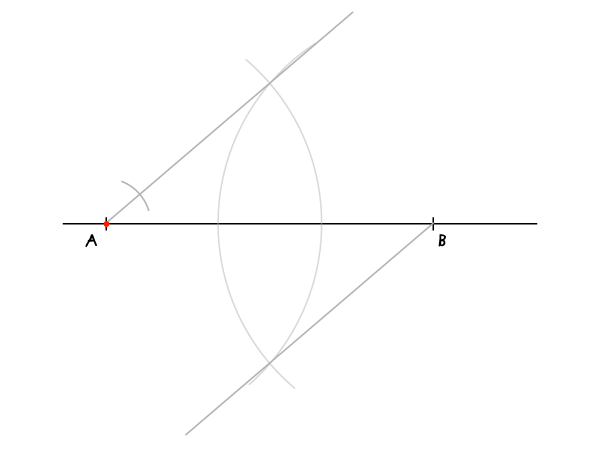
步骤4：

移动圆规的圆心到下一个标记点，按照同样半径大小画弧线，交于一点之后又继续标记下去。B点画出的平行线也是采用同样的方式。

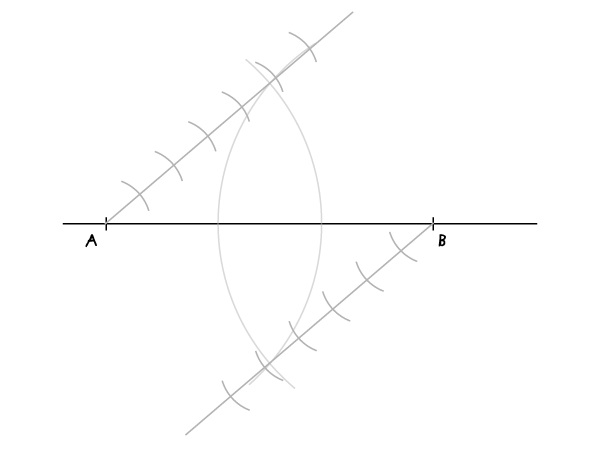
步骤5：

连接两个点，这些连接线交于这条线段后，我们可以看到这条线段已经成功被划分了七等分。