点在指定直线的投影点，即过点作一垂直于指定直线的直线，与指定直线的交点即为所求。这个问题其实回归到两条垂直直线的交点问题，回到最原始的初中几何知识，复习下

如图示

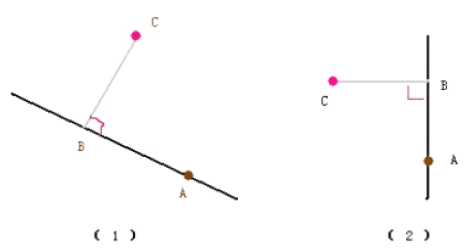
首先我们明确下已知条件，指定直线上任一点A，直线斜率k，点C，求点B

说到斜率，就有不存在的情况，如图（2），显然这种情况B的横坐标=A的横坐标，B的纵坐标=C的纵坐标

本文重点讨论第一种情况，其实也很简单，联立两条直线求解即可

直线AB方程式即y-yA=k*（x-xA）

∵两条垂直直线的斜率乘积 = -1

∴由AB线斜率为k可知BC线斜率为-1/k，可知直线BC方程式为

y-yC=-1/k*（x-xC）

联立方程组解得

xB = (k * xA+ xC / k + yC - yA) / (1 / k + k)

由xB代入BC方程即可得yB

复制代码 代码如下:

/// <summary>

/// 求直线外一点到该直线的投影点

/// </summary>

/// <param name="pLine">线上任一点</param>

/// <param name="k">直线斜率</param>

/// <param name="pOut">线外指定点</param>

/// <param name="pProject">投影点</param>

protected void GetProjectivePoint(PointF pLine, double k, PointF pOut, ref PointF pProject)

{

if (k == 0) //垂线斜率不存在情况

{

pProject.X = pOut.X;

pProject.Y = pLine.Y;

}

else

{

pProject.X = (float)((k * pLine.X + pOut.X / k + pOut.Y - pLine.Y) / (1 / k + k));

pProject.Y = (float)(-1 / k * (pProject.X - pOut.X) + pOut.Y);

}

}