复制代码 代码如下:

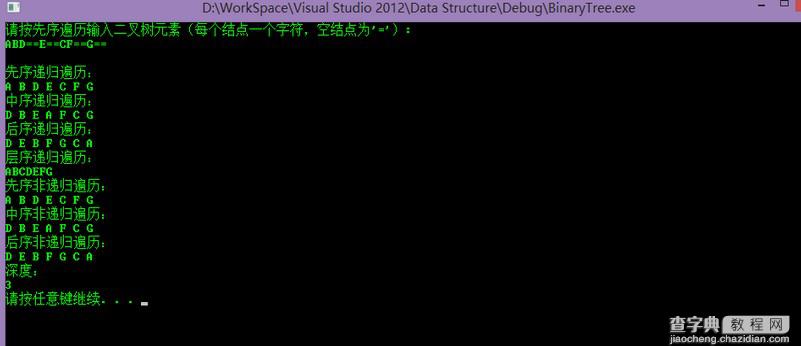
请按先序遍历输入二叉树元素（每个结点一个字符，空结点为'='）:

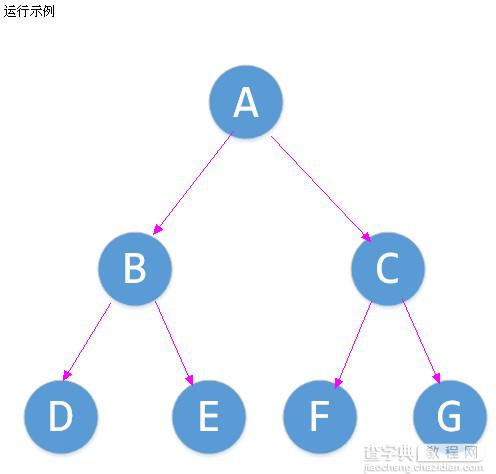
ABD==E==CF==G==

先序递归遍历：

A B D E C F G

中序递归遍历：

D B E A F C G

后序递归遍历：

D E B F G C A

层序递归遍历：

ABCDEFG

先序非递归遍历：

A B D E C F G

中序非递归遍历：

D B E A F C G

后序非递归遍历：

D E B F G C A

深度：

请按任意键继续. . .

复制代码 代码如下:

#include<stdio.h>

#include<stdlib.h>

#define OK 1

#define ERROR 0

#define TRUE 1

#define FALSE 0

#define OVERFLOW -1

#define STACK_INIT_SIZE 100

#define STACKINCREMENT 10

typedef int Status;

typedef char ElemType;

typedef struct BTNode

{

ElemType data;

struct BTNode *leftChild;

struct BTNode *rightChild;

}BTNode, *BinTree;

typedef BinTree SElemType;

typedef struct{//栈结构定义

SElemType *base;

SElemType *top;

int stacksize;

}SqStack;

BinTree CreateBinTree(BinTree T);

Status Visit(ElemType e);

Status Depth(BinTree T);

Status PreOrderRecursionTraverse(BinTree T, Status (*Visit)(ElemType e));

Status InOrderRecursionTraverse(BinTree T, Status (*Visit)(ElemType e));

Status PostOrderRecursionTraverse(BinTree T, Status (*Visit)(ElemType e));

Status LevelOrderRecursionTraverse(BinTree T, Status (*Visit)(ElemType e));

//定义栈的相关操作

Status InitStack(SqStack *S);

Status DestroyStack(SqStack *S);

Status ClearStack(SqStack *S);

Status StackEmpty(SqStack S);

int StackLength(SqStack S);

Status GetTop(SqStack S,SElemType *e);

Status Push(SqStack *S,SElemType e);

Status Pop(SqStack *S,SElemType *e);

Status StackTraverse(const SqStack *S);

Status PreOrderNoneRecursionTraverse(BinTree T, Status (*Visit)(ElemType e));

Status InOrderNoneRecursionTraverse(BinTree T, Status (*Visit)(ElemType e));

Status PostOrderNoneRecursionTraverse(BinTree T, Status (*Visit)(ElemType e));

int main()

{

int depth;

BinTree Tree = NULL;

Status(*visit)(ElemType e) = Visit;

printf_s("请按先序遍历输入二叉树元素（每个结点一个字符，空结点为'='）:n");

Tree = CreateBinTree(Tree);

printf_s("n先序递归遍历：n");

PreOrderRecursionTraverse(Tree,visit);

printf_s("n中序递归遍历：n");

InOrderRecursionTraverse(Tree,visit);

printf_s("n后序递归遍历：n");

PostOrderRecursionTraverse(Tree,visit);

printf_s("n层序递归遍历：n");

LevelOrderRecursionTraverse(Tree,visit);

printf_s("n先序非递归遍历：n");

PreOrderNoneRecursionTraverse(Tree,visit);

printf_s("n中序非递归遍历：n");

InOrderNoneRecursionTraverse(Tree,visit);

printf_s("n后序非递归遍历：n");

PostOrderNoneRecursionTraverse(Tree,visit);

printf_s("n深度：n");

depth = Depth(Tree);

printf_s("%dn", depth);

system("pause");

return 0;

}

//创建二叉树

BinTree CreateBinTree(BinTree T)

{

char ch;

scanf_s("%c", &ch);

if (ch == '=')

{

T = NULL;

}

else

{

if (!(T=(BTNode *) malloc(sizeof(BTNode))))

{

exit(OVERFLOW);

}

T->data = ch; //生成根结点

T->leftChild = CreateBinTree(T->leftChild);

T->rightChild = CreateBinTree(T->rightChild);

}

return T;

}

//访问二叉树

Status Visit(ElemType e)

{

if (e == '')

{

return ERROR;

}

else

{

printf_s("%c ", e);

}

return OK;

}

//先序遍历递归算法

Status PreOrderRecursionTraverse(BinTree T, Status (*Visit)(ElemType e))

{

if (T)

{

if (!Visit(T->data))

{

return ERROR;

}

PreOrderRecursionTraverse(T->leftChild, Visit);

PreOrderRecursionTraverse(T->rightChild, Visit);

}

return OK;

}

//中序遍历递归算法

Status InOrderRecursionTraverse(BinTree T, Status (*Visit)(ElemType e))

{

if (T)

{

InOrderRecursionTraverse(T->leftChild, Visit);

if (!Visit(T->data))

{

return ERROR;

}

InOrderRecursionTraverse(T->rightChild, Visit);

}

return OK;

}

//后序遍历递归算法

Status PostOrderRecursionTraverse(BinTree T, Status (*Visit)(ElemType e))

{

if (T)

{

PostOrderRecursionTraverse(T->leftChild, Visit);

PostOrderRecursionTraverse(T->rightChild, Visit);

if (!Visit(T->data))

{

return ERROR;

}

}

return OK;

}

//层序遍历递归算法

Status LevelOrderRecursionTraverse(BinTree T, Status (*Visit)(ElemType e))

{

if (T)

{

BTNode *Q[100];//假设不溢出

int front = -1,rear = -1;

if (T)

{

Q[++rear] = T;

printf_s("%c", T->data);

while (front != rear)

{

BTNode *p;

if (!(p = (BTNode *)malloc(sizeof(BTNode))))

{

exit(OVERFLOW);

}

p = Q[++front];

if (p->leftChild)

{

Q[++rear] = p->leftChild;

printf("%c",p->leftChild->data);

}

if (p->rightChild)

{

Q[++rear] = p->rightChild;

printf("%c",p->rightChild->data);

}

}

}

}

return OK;

}

Status Depth(BinTree T)

{

int a,b;

if (!T)

{

return ERROR;

}

else

{

a = Depth(T->leftChild) + 1;

b = Depth(T->rightChild) + 1;

return a > b ? a : b;

}

}

//先序遍历非递归算法

Status PreOrderNoneRecursionTraverse(BinTree T, Status (*Visit)(ElemType e))

{

SqStack S;

SElemType p;

InitStack(&S);

Push(&S, T);

while (!StackEmpty(S))

{

Pop(&S, &p);

if (!Visit(p->data))

{

return ERROR;

}

if (p->leftChild)

{

Push(&S, p->rightChild);

}

if (p->rightChild)

{

Push(&S, p->leftChild);

}

}

DestroyStack(&S);

return OK;

}

//中序遍历非递归算法

Status InOrderNoneRecursionTraverse(BinTree T, Status (*Visit)(ElemType e))

{

SqStack S;

SElemType p;

InitStack(&S);

Push(&S, T);

while (!StackEmpty(S))

{

while (GetTop(S,&p) && p)

{

Push(&S, p->leftChild);

}

Pop(&S, &p);

if (!StackEmpty(S))

{

Pop(&S, &p);

if (!Visit(p->data))

{

return ERROR;

}

Push(&S, p->rightChild);

}

}

DestroyStack(&S);

return OK;

}

//后序便利非递归算法

Status PostOrderNoneRecursionTraverse(BinTree T, Status (*Visit)(ElemType e))

{

SqStack S;

SElemType p, q;

InitStack(&S);

Push(&S,T);

while(!StackEmpty(S))

{

while(GetTop(S,&p)&&p&&(p->leftChild||p->rightChild))

{

Push(&S,p->rightChild);

Push(&S,p->leftChild);

}

if(!StackEmpty(S)){

Pop(&S,&p);

if (p)

{

if(!Visit(p->data))

{

return ERROR;

}

}

else

{

Pop(&S,&p);

if(!Visit(p->data))

{

return ERROR;

}

}

while (GetTop(S,&q)&&q&&p==q->rightChild)

{

Pop(&S,&p);

if(!Visit(p->data))

{

return ERROR;

}

GetTop(S,&q);

}

}

}

DestroyStack(&S);

return OK;

}

//-----------栈的相关操作--------------//

Status InitStack(SqStack *S){

S->base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType));

if(!S->base)

{

exit(0);

}

S->top = S->base;

S->stacksize = STACK_INIT_SIZE;

return OK;

}

Status DestroyStack(SqStack *S){

if(!S)

{

exit(0);

}

free(S->base);

return OK;

}

Status ClearStack(SqStack *S){

if(!S)

{

return FALSE;

}

S->top = S->base;

return OK;

}

Status StackEmpty(SqStack S){

if(S.top==S.base)

{

return TRUE;

}

else

{

return FALSE;

}

}

int StackLength(SqStack S){

return S.stacksize;

}

Status GetTop(SqStack S,SElemType *e){

if(S.top == S.base)

{

return FALSE;

}

else

{

*e = *(S.top-1);

return OK;

}

}

Status Push(SqStack *S,SElemType e){

if(S->top-S->base>=S->stacksize)

{

S->base = (SElemType *)realloc(S->base, (S->stacksize + STACKINCREMENT) * sizeof(SElemType));

if(!S->base)

{

exit(0);

}

S->top = S->base+S->stacksize;

S->stacksize += STACKINCREMENT;

}

*S->top++ = e;

return OK;

}

Status Pop(SqStack *S,SElemType *e){

if(S->top==S->base)

{

return ERROR;

}

*e = *(--S->top);

return OK;

}