听说赫夫曼胜过了他的导师,被认为”青出于蓝而胜于蓝“,这句话也是我比较欣赏的,嘻嘻。
一 概念
了解”赫夫曼树“之前,几个必须要知道的专业名词可要熟练记住啊。
1: 结点的权
“权”就相当于“重要度”,我们形象的用一个具体的数字来表示,然后通过数字的大小来决定谁重要,谁不重要。
2: 路径
树中从“一个结点"到“另一个结点“之间的分支。
3: 路径长度
一个路径上的分支数量。
4: 树的路径长度
从树的根节点到每个节点的路径长度之和。
5: 节点的带权路径路劲长度
其实也就是该节点到根结点的路径长度*该节点的权。
6: 树的带权路径长度
树中各个叶节点的路径长度*该叶节点的权的和,常用WPL(Weight Path Length)表示。
二: 构建赫夫曼树
上面说了那么多,肯定是为下面做铺垫,这里说赫夫曼树,肯定是要说赫夫曼树咋好咋好,赫夫曼树是一种最优二叉树,
因为他的WPL是最短的,何以见得?我们可以上图说话。
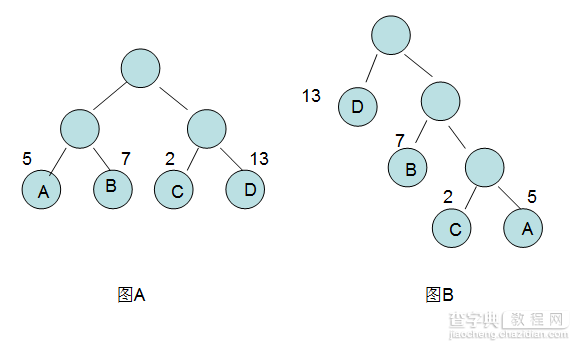
现在我们做一个WPL的对比:
图A: WPL= 5*2 + 7*2 +2*2+13*2=54
图B:WPL=5*3+2*3+7*2+13*1=48
我们对比一下,图B的WPL最短的,地球人已不能阻止WPL还能比“图B”的小,所以,“图B"就是一颗赫夫曼树,那么大家肯定
要问,如何构建一颗赫夫曼树,还是上图说话。
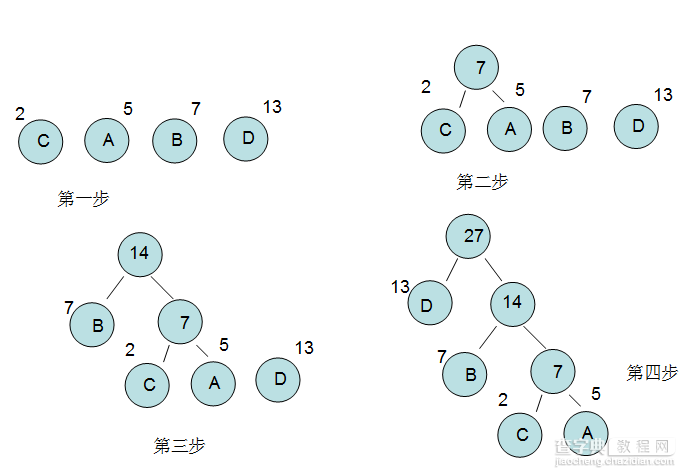
第一步: 我们将所有的节点都作为独根结点。
第二步: 我们将最小的C和A组建为一个新的二叉树,权值为左右结点之和。
第三步: 将上一步组建的新节点加入到剩下的节点中,排除上一步组建过的左右子树,我们选中B组建新的二叉树,然后取权值。
第四步: 同上。
三: 赫夫曼编码
大家都知道,字符,汉字,数字在计算机中都是以0,1来表示的,相应的存储都是有一套编码方案来支撑的,比如ASC码。
这样才能在"编码“和”解码“的过程中不会成为乱码,但是ASC码不理想的地方就是等长的,其实我们都想用较少的空间来存储
更多的东西,那么我们就要采用”不等长”的编码方案来存储,那么“何为不等长呢“?其实也就是出现次数比较多的字符我们采用短编码,
出现次数较少的字符我们采用长编码,恰好,“赫夫曼编码“就是不等长的编码。
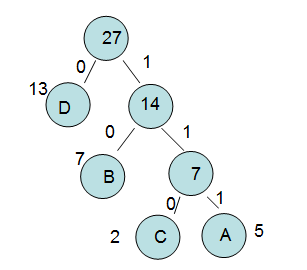
这里大家只要掌握赫夫曼树的编码规则:左子树为0,右子树为1,对应的编码后的规则是:从根节点到子节点
A: 111
B: 10
C: 110
D: 0
四: 实现
不知道大家懂了没有,不懂的话多看几篇,下面说下赫夫曼的具体实现。
第一步:构建赫夫曼树。
第二步:对赫夫曼树进行编码。
第三步:压缩操作。
第四步:解压操作。
1:首先看下赫夫曼树的结构,这里字段的含义就不解释了。
复制代码 代码如下:
#region 赫夫曼树结构
/// <summary>
/// 赫夫曼树结构
/// </summary>
public class HuffmanTree
{
public int weight { get; set; }
public int parent { get; set; }
public int left { get; set; }
public int right { get; set; }
}
#endregion
2: 创建赫夫曼树,原理在上面已经解释过了,就是一步一步的向上搭建,这里要注意的二个性质定理:
当叶子节点为N个,则需要N-1步就能搭建赫夫曼树。
当叶子节点为N个,则赫夫曼树的节点总数为:(2*N)-1个。
复制代码 代码如下:
#region 赫夫曼树的创建
/// <summary>
/// 赫夫曼树的创建
/// </summary>
/// <param name="huffman">赫夫曼树</param>
/// <param name="leafNum">叶子节点</param>
/// <param name="weight">节点权重</param>
public HuffmanTree[] CreateTree(HuffmanTree[] huffman, int leafNum, int[] weight)
{
//赫夫曼树的节点总数
int huffmanNode = 2 * leafNum - 1;
//初始化节点,赋予叶子节点值
for (int i = 0; i < huffmanNode; i++)
{
if (i < leafNum)
{
huffman[i].weight = weight[i];
}
}
//这里面也要注意,4个节点,其实只要3步就可以构造赫夫曼树
for (int i = leafNum; i < huffmanNode; i++)
{
int minIndex1;
int minIndex2;
SelectNode(huffman, i, out minIndex1, out minIndex2);
//最后得出minIndex1和minindex2中实体的weight最小
huffman[minIndex1].parent = i;
huffman[minIndex2].parent = i;
huffman[i].left = minIndex1;
huffman[i].right = minIndex2;
huffman[i].weight = huffman[minIndex1].weight + huffman[minIndex2].weight;
}
return huffman;
}
#endregion
#region 选出叶子节点中最小的二个节点
/// <summary>
/// 选出叶子节点中最小的二个节点
/// </summary>
/// <param name="huffman"></param>
/// <param name="searchNodes">要查找的结点数</param>
/// <param name="minIndex1"></param>
/// <param name="minIndex2"></param>
public void SelectNode(HuffmanTree[] huffman, int searchNodes, out int minIndex1, out int minIndex2)
{
HuffmanTree minNode1 = null;
HuffmanTree minNode2 = null;
//最小节点在赫夫曼树中的下标
minIndex1 = minIndex2 = 0;
//查找范围
for (int i = 0; i < searchNodes; i++)
{
///只有独根树才能进入查找范围
if (huffman[i].parent == 0)
{
//如果为null,则认为当前实体为最小
if (minNode1 == null)
{
minIndex1 = i;
minNode1 = huffman[i];
continue;
}
//如果为null,则认为当前实体为最小
if (minNode2 == null)
{
minIndex2 = i;
minNode2 = huffman[i];
//交换一个位置,保证minIndex1为最小,为后面判断做准备
if (minNode1.weight > minNode2.weight)
{
//节点交换
var temp = minNode1;
minNode1 = minNode2;
minNode2 = temp;
//下标交换
var tempIndex = minIndex1;
minIndex1 = minIndex2;
minIndex2 = tempIndex;
continue;
}
}
if (minNode1 != null && minNode2 != null)
{
if (huffman[i].weight <= minNode1.weight)
{
//将min1临时转存给min2
minNode2 = minNode1;
minNode1 = huffman[i];
//记录在数组中的下标
minIndex2 = minIndex1;
minIndex1 = i;
}
else
{
if (huffman[i].weight < minNode2.weight)
{
minNode2 = huffman[i];
minIndex2 = i;
}
}
}
}
}
}
#endregion
3:对哈夫曼树进行编码操作,形成一套“模板”,效果跟ASC模板一样,不过一个是不等长,一个是等长。
复制代码 代码如下:
#region 赫夫曼编码
/// <summary>
/// 赫夫曼编码
/// </summary>
/// <param name="huffman"></param>
/// <param name="leafNum"></param>
/// <param name="huffmanCode"></param>
public string[] HuffmanCoding(HuffmanTree[] huffman, int leafNum)
{
int current = 0;
int parent = 0;
string[] huffmanCode = new string[leafNum];
//四个叶子节点的循环
for (int i = 0; i < leafNum; i++)
{
//单个字符的编码串
string codeTemp = string.Empty;
current = i;
//第一次获取最左节点
parent = huffman[current].parent;
while (parent != 0)
{
//如果父节点的左子树等于当前节点就标记为0
if (current == huffman[parent].left)
codeTemp += "0";
else
codeTemp += "1";
current = parent;
parent = huffman[parent].parent;
}
huffmanCode[i] = new string(codeTemp.Reverse().ToArray());
}
return huffmanCode;
}
#endregion
4:模板生成好了,我们就要对指定的测试数据进行压缩处理
复制代码 代码如下:
#region 对指定字符进行压缩
/// <summary>
/// 对指定字符进行压缩
/// </summary>
/// <param name="huffmanCode"></param>
/// <param name="alphabet"></param>
/// <param name="test"></param>
public string Encode(string[] huffmanCode, string[] alphabet, string test)
{
//返回的0,1代码
string encodeStr = string.Empty;
//对每个字符进行编码
for (int i = 0; i < test.Length; i++)
{
//在模版里面查找
for (int j = 0; j < alphabet.Length; j++)
{
if (test[i].ToString() == alphabet[j])
{
encodeStr += huffmanCode[j];
}
}
}
return encodeStr;
}
#endregion
5: 最后也就是对压缩的数据进行还原操作。
复制代码 代码如下:
#region 对指定的二进制进行解压
/// <summary>
/// 对指定的二进制进行解压
/// </summary>
/// <param name="huffman"></param>
/// <param name="leafNum"></param>
/// <param name="alphabet"></param>
/// <param name="test"></param>
/// <returns></returns>
public string Decode(HuffmanTree[] huffman, int huffmanNodes, string[] alphabet, string test)
{
string decodeStr = string.Empty;
//所有要解码的字符
for (int i = 0; i < test.Length; )
{
int j = 0;
//赫夫曼树结构模板(用于循环的解码单个字符)
for (j = huffmanNodes - 1; (huffman[j].left != 0 || huffman[j].right != 0); )
{
if (test[i].ToString() == "0")
{
j = huffman[j].left;
}
if (test[i].ToString() == "1")
{
j = huffman[j].right;
}
i++;
}
decodeStr += alphabet[j];
}
return decodeStr;
}
#endregion
最后上一下总的运行代码
复制代码 代码如下:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace HuffmanTree
{
class Program
{
static void Main(string[] args)
{
//有四个叶节点
int leafNum = 4;
//赫夫曼树中的节点总数
int huffmanNodes = 2 * leafNum - 1;
//各节点的权值
int[] weight = { 5, 7, 2, 13 };
string[] alphabet = { "A", "B", "C", "D" };
string testCode = "DBDBDABDCDADBDADBDADACDBDBD";
//赫夫曼树用数组来保存,每个赫夫曼都作为一个实体存在
HuffmanTree[] huffman = new HuffmanTree[huffmanNodes].Select(i => new HuffmanTree() { }).ToArray();
HuffmanTreeManager manager = new HuffmanTreeManager();
manager.CreateTree(huffman, leafNum, weight);
string[] huffmanCode = manager.HuffmanCoding(huffman, leafNum);
for (int i = 0; i < leafNum; i++)
{
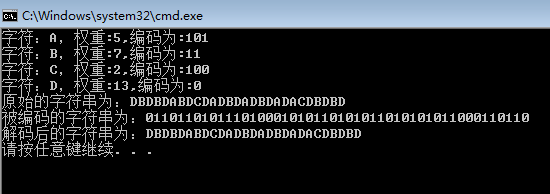
Console.WriteLine("字符:{0},权重:{1},编码为:{2}", alphabet[i], huffman[i].weight, huffmanCode[i]);
}
Console.WriteLine("原始的字符串为:" + testCode);
string encode = manager.Encode(huffmanCode, alphabet, testCode);
Console.WriteLine("被编码的字符串为:" + encode);
string decode = manager.Decode(huffman, huffmanNodes, alphabet, encode);
Console.WriteLine("解码后的字符串为:" + decode);
}
}
#region 赫夫曼树结构
/// <summary>
/// 赫夫曼树结构
/// </summary>
public class HuffmanTree
{
public int weight { get; set; }
public int parent { get; set; }
public int left { get; set; }
public int right { get; set; }
}
#endregion
/// <summary>
/// 赫夫曼树的操作类
/// </summary>
public class HuffmanTreeManager
{
#region 赫夫曼树的创建
/// <summary>
/// 赫夫曼树的创建
/// </summary>
/// <param name="huffman">赫夫曼树</param>
/// <param name="leafNum">叶子节点</param>
/// <param name="weight">节点权重</param>
public HuffmanTree[] CreateTree(HuffmanTree[] huffman, int leafNum, int[] weight)
{
//赫夫曼树的节点总数
int huffmanNode = 2 * leafNum - 1;
//初始化节点,赋予叶子节点值
for (int i = 0; i < huffmanNode; i++)
{
if (i < leafNum)
{
huffman[i].weight = weight[i];
}
}
//这里面也要注意,4个节点,其实只要3步就可以构造赫夫曼树
for (int i = leafNum; i < huffmanNode; i++)
{
int minIndex1;
int minIndex2;
SelectNode(huffman, i, out minIndex1, out minIndex2);
//最后得出minIndex1和minindex2中实体的weight最小
huffman[minIndex1].parent = i;
huffman[minIndex2].parent = i;
huffman[i].left = minIndex1;
huffman[i].right = minIndex2;
huffman[i].weight = huffman[minIndex1].weight + huffman[minIndex2].weight;
}
return huffman;
}
#endregion
#region 选出叶子节点中最小的二个节点
/// <summary>
/// 选出叶子节点中最小的二个节点
/// </summary>
/// <param name="huffman"></param>
/// <param name="searchNodes">要查找的结点数</param>
/// <param name="minIndex1"></param>
/// <param name="minIndex2"></param>
public void SelectNode(HuffmanTree[] huffman, int searchNodes, out int minIndex1, out int minIndex2)
{
HuffmanTree minNode1 = null;
HuffmanTree minNode2 = null;
//最小节点在赫夫曼树中的下标
minIndex1 = minIndex2 = 0;
//查找范围
for (int i = 0; i < searchNodes; i++)
{
///只有独根树才能进入查找范围
if (huffman[i].parent == 0)
{
//如果为null,则认为当前实体为最小
if (minNode1 == null)
{
minIndex1 = i;
minNode1 = huffman[i];
continue;
}
//如果为null,则认为当前实体为最小
if (minNode2 == null)
{
minIndex2 = i;
minNode2 = huffman[i];
//交换一个位置,保证minIndex1为最小,为后面判断做准备
if (minNode1.weight > minNode2.weight)
{
//节点交换
var temp = minNode1;
minNode1 = minNode2;
minNode2 = temp;
//下标交换
var tempIndex = minIndex1;
minIndex1 = minIndex2;
minIndex2 = tempIndex;
continue;
}
}
if (minNode1 != null && minNode2 != null)
{
if (huffman[i].weight <= minNode1.weight)
{
//将min1临时转存给min2
minNode2 = minNode1;
minNode1 = huffman[i];
//记录在数组中的下标
minIndex2 = minIndex1;
minIndex1 = i;
}
else
{
if (huffman[i].weight < minNode2.weight)
{
minNode2 = huffman[i];
minIndex2 = i;
}
}
}
}
}
}
#endregion
#region 赫夫曼编码
/// <summary>
/// 赫夫曼编码
/// </summary>
/// <param name="huffman"></param>
/// <param name="leafNum"></param>
/// <param name="huffmanCode"></param>
public string[] HuffmanCoding(HuffmanTree[] huffman, int leafNum)
{
int current = 0;
int parent = 0;
string[] huffmanCode = new string[leafNum];
//四个叶子节点的循环
for (int i = 0; i < leafNum; i++)
{
//单个字符的编码串
string codeTemp = string.Empty;
current = i;
//第一次获取最左节点
parent = huffman[current].parent;
while (parent != 0)
{
//如果父节点的左子树等于当前节点就标记为0
if (current == huffman[parent].left)
codeTemp += "0";
else
codeTemp += "1";
current = parent;
parent = huffman[parent].parent;
}
huffmanCode[i] = new string(codeTemp.Reverse().ToArray());
}
return huffmanCode;
}
#endregion
#region 对指定字符进行压缩
/// <summary>
/// 对指定字符进行压缩
/// </summary>
/// <param name="huffmanCode"></param>
/// <param name="alphabet"></param>
/// <param name="test"></param>
public string Encode(string[] huffmanCode, string[] alphabet, string test)
{
//返回的0,1代码
string encodeStr = string.Empty;
//对每个字符进行编码
for (int i = 0; i < test.Length; i++)
{
//在模版里面查找
for (int j = 0; j < alphabet.Length; j++)
{
if (test[i].ToString() == alphabet[j])
{
encodeStr += huffmanCode[j];
}
}
}
return encodeStr;
}
#endregion
#region 对指定的二进制进行解压
/// <summary>
/// 对指定的二进制进行解压
/// </summary>
/// <param name="huffman"></param>
/// <param name="leafNum"></param>
/// <param name="alphabet"></param>
/// <param name="test"></param>
/// <returns></returns>
public string Decode(HuffmanTree[] huffman, int huffmanNodes, string[] alphabet, string test)
{
string decodeStr = string.Empty;
//所有要解码的字符
for (int i = 0; i < test.Length; )
{
int j = 0;
//赫夫曼树结构模板(用于循环的解码单个字符)
for (j = huffmanNodes - 1; (huffman[j].left != 0 || huffman[j].right != 0); )
{
if (test[i].ToString() == "0")
{
j = huffman[j].left;
}
if (test[i].ToString() == "1")
{
j = huffman[j].right;
}
i++;
}
decodeStr += alphabet[j];
}
return decodeStr;
}
#endregion
}
}