大家是否感觉到,树在数据结构中大行其道,什么领域都要沾一沾,碰一碰。
就拿我们前几天学过的排序就用到了堆和今天讲的”二叉排序树“,所以偏激的说,掌握的树你就是牛人了。
今天就聊聊这个”五大经典查找“中的最后一个”二叉排序树“。
1. 概念:
<1> 其实很简单,若根节点有左子树,则左子树的所有节点都比根节点小。
若根节点有右子树,则右子树的所有节点都比根节点大。
<2> 如图就是一个”二叉排序树“,然后对照概念一比较比较。
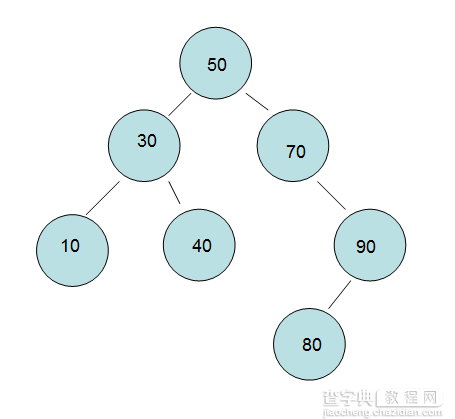
2.实际操作:
我们都知道,对一个东西进行操作,无非就是增删查改,接下来我们就聊聊其中的基本操作。
<1> 插入:相信大家对“排序树”的概念都清楚了吧,那么插入的原理就很简单了。
比如说我们插入一个20到这棵树中。
首先:20跟50比,发现20是老小,不得已,得要归结到50的左子树中去比较。
然后:20跟30比,发现20还是老小。
再然后:20跟10比,发现自己是老大,随即插入到10的右子树中。
最后: 效果呈现图如下:
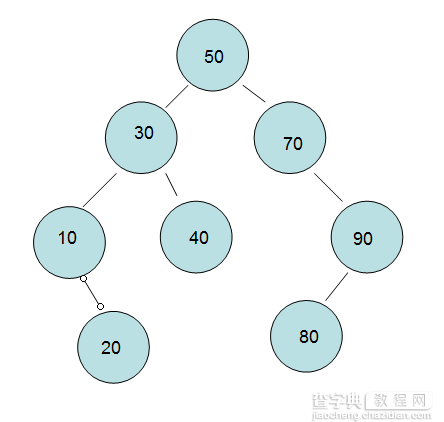
<2>查找:相信懂得了插入,查找就跟容易理解了。
就拿上面一幅图来说,比如我想找到节点10.
首先:10跟50比,发现10是老小,则在50的左子树中找。
然后:10跟30比,发现还是老小,则在30的左子树中找。
再然后: 10跟10比,发现一样,然后就返回找到的信号。
<3>删除:删除节点在树中还是比较麻烦的,主要有三种情况。
《1》 删除的是“叶节点20“,这种情况还是比较简单的,删除20不会破坏树的结构。如图:
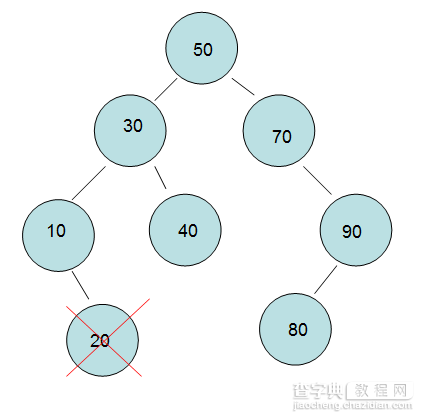
《2》删除”单孩子节点90“,这个情况相比第一种要麻烦一点点,需要把他的孩子顶上去。
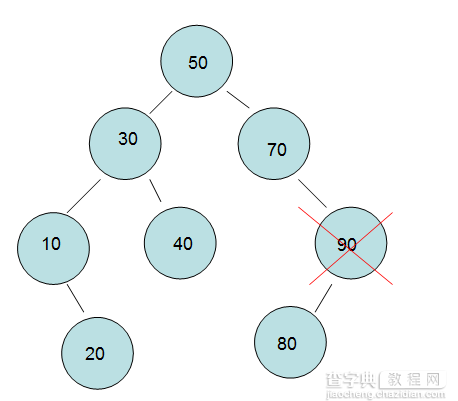
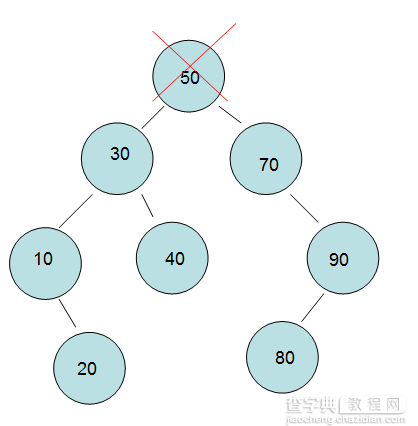
《3》删除“左右孩子都有的节点50”,这个让我在代码编写上纠结了好长时间,问题很直白,
我把50删掉了,谁顶上去了问题,是左孩子呢?还是右孩子呢?还是另有蹊跷?这里我就
坦白吧,不知道大家可否知道“二叉树”的中序遍历,不过这个我会在后面讲的,现在可以当
公式记住吧,就是找到右节点的左子树最左孩子。
比如:首先 找到50的右孩子70。
然后 找到70的最左孩子,发现没有,则返回自己。
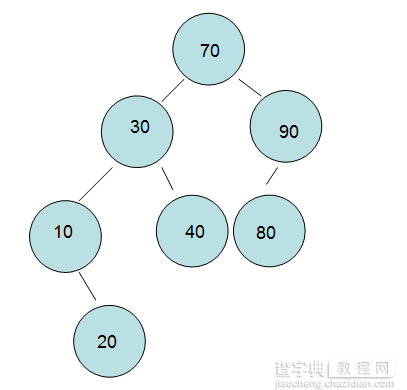
最后 原始图和最终图如下。
3.说了这么多,上代码说话。
复制代码 代码如下:
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Diagnostics;
namespace TreeSearch
{
class Program
{
static void Main(string[] args)
{
List<int> list = new List<int>() { 50, 30, 70, 10, 40, 90, 80 };
//创建二叉遍历树
BSTree bsTree = CreateBST(list);
Console.Write("中序遍历的原始数据:");
//中序遍历
LDR_BST(bsTree);
Console.WriteLine("n---------------------------------------------------------------------------n");
//查找一个节点
Console.WriteLine("n10在二叉树中是否包含:" + SearchBST(bsTree, 10));
Console.WriteLine("n---------------------------------------------------------------------------n");
bool isExcute = false;
//插入一个节点
InsertBST(bsTree, 20, ref isExcute);
Console.WriteLine("n20插入到二叉树,中序遍历后:");
//中序遍历
LDR_BST(bsTree);
Console.WriteLine("n---------------------------------------------------------------------------n");
Console.Write("删除叶子节点 20, n中序遍历后:");
//删除一个节点(叶子节点)
DeleteBST(ref bsTree, 20);
//再次中序遍历
LDR_BST(bsTree);
Console.WriteLine("n****************************************************************************n");
Console.WriteLine("删除单孩子节点 90, n中序遍历后:");
//删除单孩子节点
DeleteBST(ref bsTree, 90);
//再次中序遍历
LDR_BST(bsTree);
Console.WriteLine("n****************************************************************************n");
Console.WriteLine("删除根节点 50, n中序遍历后:");
//删除根节点
DeleteBST(ref bsTree, 50);
LDR_BST(bsTree);
}
///<summary>
/// 定义一个二叉排序树结构
///</summary>
public class BSTree
{
public int data;
public BSTree left;
public BSTree right;
}
///<summary>
/// 二叉排序树的插入操作
///</summary>
///<param name="bsTree">排序树</param>
///<param name="key">插入数</param>
///<param name="isExcute">是否执行了if语句</param>
static void InsertBST(BSTree bsTree, int key, ref bool isExcute)
{
if (bsTree == null)
return;
//如果父节点大于key,则遍历左子树
if (bsTree.data > key)
InsertBST(bsTree.left, key, ref isExcute);
else
InsertBST(bsTree.right, key, ref isExcute);
if (!isExcute)
{
//构建当前节点
BSTree current = new BSTree()
{
data = key,
left = null,
right = null
};
//插入到父节点的当前元素
if (bsTree.data > key)
bsTree.left = current;
else
bsTree.right = current;
isExcute = true;
}
}
///<summary>
/// 创建二叉排序树
///</summary>
///<param name="list"></param>
static BSTree CreateBST(List<int> list)
{
//构建BST中的根节点
BSTree bsTree = new BSTree()
{
data = list[0],
left = null,
right = null
};
for (int i = 1; i < list.Count; i++)
{
bool isExcute = false;
InsertBST(bsTree, list[i], ref isExcute);
}
return bsTree;
}
///<summary>
/// 在排序二叉树中搜索指定节点
///</summary>
///<param name="bsTree"></param>
///<param name="key"></param>
///<returns></returns>
static bool SearchBST(BSTree bsTree, int key)
{
//如果bsTree为空,说明已经遍历到头了
if (bsTree == null)
return false;
if (bsTree.data == key)
return true;
if (bsTree.data > key)
return SearchBST(bsTree.left, key);
else
return SearchBST(bsTree.right, key);
}
///<summary>
/// 中序遍历二叉排序树
///</summary>
///<param name="bsTree"></param>
///<returns></returns>
static void LDR_BST(BSTree bsTree)
{
if (bsTree != null)
{
//遍历左子树
LDR_BST(bsTree.left);
//输入节点数据
Console.Write(bsTree.data + "");
//遍历右子树
LDR_BST(bsTree.right);
}
}
///<summary>
/// 删除二叉排序树中指定key节点
///</summary>
///<param name="bsTree"></param>
///<param name="key"></param>
static void DeleteBST(ref BSTree bsTree, int key)
{
if (bsTree == null)
return;
if (bsTree.data == key)
{
//第一种情况:叶子节点
if (bsTree.left == null && bsTree.right == null)
{
bsTree = null;
return;
}
//第二种情况:左子树不为空
if (bsTree.left != null && bsTree.right == null)
{
bsTree = bsTree.left;
return;
}
//第三种情况,右子树不为空
if (bsTree.left == null && bsTree.right != null)
{
bsTree = bsTree.right;
return;
}
//第四种情况,左右子树都不为空
if (bsTree.left != null && bsTree.right != null)
{
var node = bsTree.right;
//找到右子树中的最左节点
while (node.left != null)
{
//遍历它的左子树
node = node.left;
}
//交换左右孩子
node.left = bsTree.left;
//判断是真正的叶子节点还是空左孩子的父节点
if (node.right == null)
{
//删除掉右子树最左节点
DeleteBST(ref bsTree, node.data);
node.right = bsTree.right;
}
//重新赋值一下
bsTree = node;
}
}
if (bsTree.data > key)
{
DeleteBST(ref bsTree.left, key);
}
else
{
DeleteBST(ref bsTree.right, key);
}
}
}
}
运行结果:
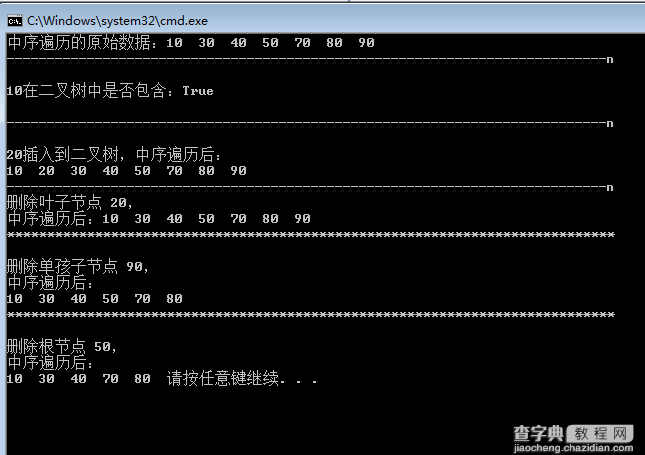
值的注意的是:二叉排序树同样采用“空间换时间”的做法。
突然发现,二叉排序树的中序遍历同样可以排序数组,呵呵,不错!
PS: 插入操作:O(LogN)。
删除操作:O(LogN)。
查找操作:O(LogN)。


