首先,明白什么是双向链表。所谓双向链表是如果希望找直接前驱结点和直接后继结点的时间复杂度都是 O(1),那么,需要在结点中设两个引用域,一个保存直接前驱结点的地址,叫 prev,一个直接后继结点的地址,叫 next,这样的链表就是双向链表(Doubly Linked List)。双向链表的结点结构示意图如图所示。

双向链表结点的定义与单链表的结点的定义很相似, ,只是双向链表多了一个字段 prev。其实,双向链表更像是一根链条一样,你连我,我连你,不清楚,请看图。

双向链表结点类的实现如下所示
//一个链条的类
public class DbNode<T>
{
//当前的数据所在
private T data; //数据域记录的数据的
private DbNode<T> prev; //前驱引用域 前驱 引用位置
private DbNode<T> next; //后继引用域 后来链条的位置
//构造器 这是不是初始化
public DbNode(T val, DbNode<T> p)
{
data = val;
next = p;
}
//构造器 这是不是初始化
public DbNode(DbNode<T> p)
{
next = p;
}
//构造器 吧这个链子相应值 传递给他
public DbNode(T val)
{
data = val;
next = null;
}
//构造器 构造一个空的链子
public DbNode()
{
data = default(T);
next = null;
}
//数据域属性
public T Data
{
get
{
return data;
}
set
{
data = value;
}
}
//前驱引用域属性
public DbNode<T> Prev
{
get
{
return prev;
}
set
{
prev = value;
}
}
//后继引用域属性
public DbNode<T> Next
{
get
{
return next;
}
set
{
next = value;
}
}
}
说了这么多双向链表接点的类的属性,我们要看一看他的相关的操作。这里只做一些画龙点睛地方的描述
插入操作:设 p是指向双向链表中的某一结点,即 p存储的是该结点的地址,现要将一个结点 s 插入到结点 p 的后面,插入的源代码如下所示:操作如下:
➀ p.Next.Prev = s;
➁ s.Prev = p;
➂ s.Next = p.Next;
➃ p.Next = s;
插入过程如图所示(以 p 的直接后继结点存在为例) 。
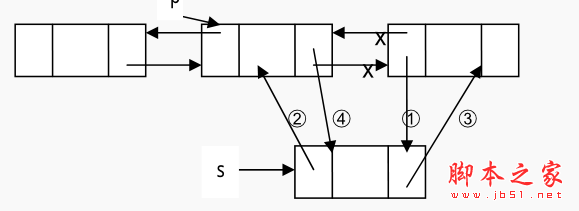
注意:引用域值的操作的顺序不是唯一的,但也不是任意的,操作➂必须放到操作➃的前面完成,否则 p 直接后继结点的就找不到了。这一点需要读者把每个操作的含义搞清楚。此算法时间操作消耗在查找上,其时间的复杂度是O(n).
下面,看他的删除操作,以在结点之后删除为例来说明在双向链表中删除结点的情况。 设 p是指向双向链表中的某一结点,即 p存储的是该结点的地址,现要将一个结点 s插入到结点 p的后面 。伪代码如下:操作如下:
➀ p.Next = P.Next.Next;
➁ p.Next.Prev = p.Prev;
删除过程如图所示(以 p的直接后继结点存在为例)
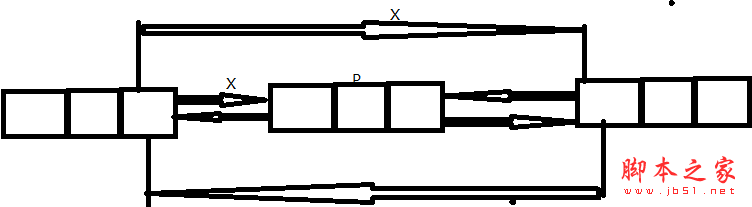
相应的算法的时间复杂度也是消耗到结点的查找上,其复杂度应该是O(n)
查找操作与单链表的极其的类似,也是从头开始遍历。相应伪代码如图所示:
current.next=p.next.next
current.prev=p.next.prev;
相应的伪代码如下图所示:
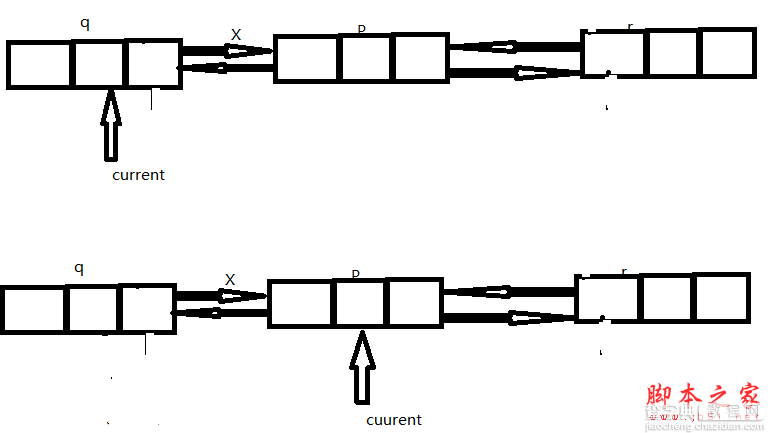
该算法的时间复杂度,是一个个的遍历的过程中,顾时间复杂度是O(n)
获取当前的双向链表长度与 查找类似,不做过多的赘述,这里,我们把双向链表基本概念和操作基本介绍完了,下面介绍一个重要的链表——环形链表。
首先,还是老样子,看看环形链表的定义。有些应用不需要链表中有明显的头尾结点。在这种情况下,可能需要方便地从最后一个结点访问到第一个结点。此时,最后一个结点的引用域不是空引用,而是保存的第一个结点的地址(如果该链表带结点,则保存的是头结点的地址) ,也就是头引用的值。我们把这样的链表结构称之为环形链表。他就像小朋友手拉手做游戏。如图所示。
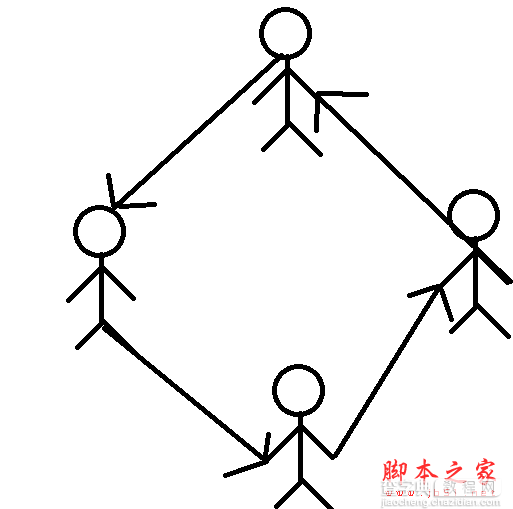
用链表如图所示:
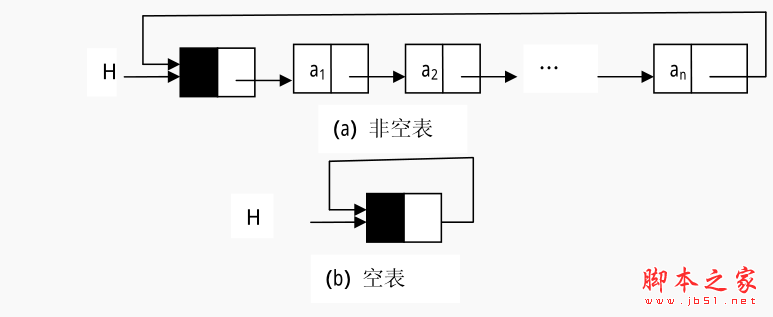
这里基本添加,删除,操作的操作与单链表简直是一模一样,这里就没有必要写这些东西。我们主要看他们一些简单应用。
应用举例一已知单链表 H,写一算法将其倒置,即实现如图所示的操作,其中(a)为倒置前,(b)为倒置后。
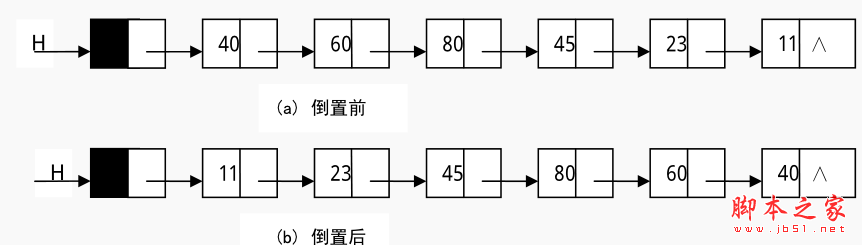
算法思路:由于单链表的存储空间不是连续的,所以,它的倒置不能像顺表那样,把第 i 个结点与第 n-i 个结点交换(i 的取值范围是 1 到 n/2,n 为单链表的长度) 。其解决办法是依次取单链表中的每个结点插入到新链表中去。并且,为了节省内存资源,把原链表的头结点作为新链表的头结点。存储整数的单链表的倒置的算法实现如下:
public void ReversLinkList(LinkList<int> H)
{
Node<int> p = H.Next;
Node<int> q = new Node<int>();
H.Next = null;
while (p != null)
{
q = p;
p = p.Next;
q.Next = H.Next;
H.Next = q;
}
}
该算法要对链表中的结点顺序扫描一遍才完成了倒置,所以时间复杂度为O(n),但比同样长度的顺序表多花一倍的时间,因为顺序表只需要扫描一半的数据元素。这个是不是你已经头脑糊了吗?如果糊了把,请看我的图例的解释。
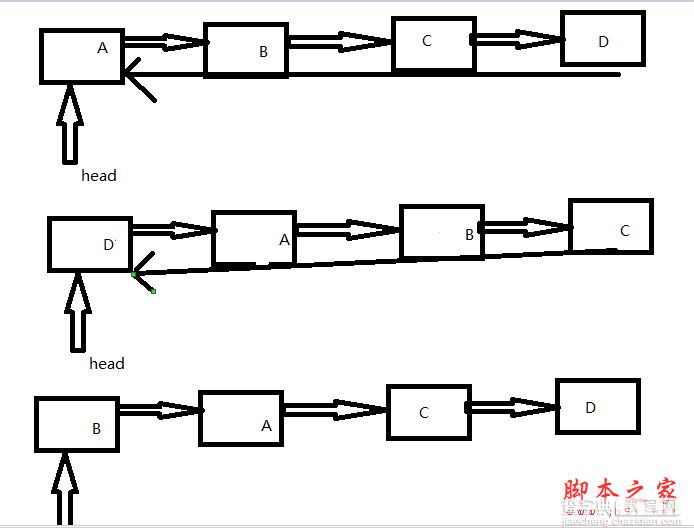
举例2,约瑟夫环问题,题目如下:
已知n个人(以编号1,2,3...n分别表示)围坐在一张圆桌周围。从编号为k的人开始报数,数到m的那个人出列;他的下一个人又从1开始报数,数到m的那个人又出列;依此规律重复下去,直到圆桌周围的人全部出列。求最后出列的人相应的编号。
void JOSEPHUS(int n,int k,int m) //n为总人数,k为第一个开始报数的人,m为出列者喊到的数
{
/* p为当前结点 r为辅助结点,指向p的前驱结点 list为头节点*/
LinkList p,r,list; /*建立循环链表*/
for(int i=0;i<n;i++)
{
p=(LinkList)LNode;
p.data=i;
if(list==NULL)
list=p;
else
r.link=p;
r=p;
}
p.link=list; /*使链表循环起来*/
p=list;/*使p指向头节点*/
/*把当前指针移动到第一个报数的人*/
for(i=0;i<k;i++)
{
r=p;
p=p.link;
}
/*循环地删除队列结点*/
while(p.link!=p)
{
for(i=0;i<m-1;i++)
{
r=p;
p=p.link;
}
r.link=p.link;
console.writeline("被删除的元素:{0} ",p.data);
free(p);
p=r.node.;
}
console.writeLine("n最后被删除的元素是:{0}",P.data);
具体的算法,如图所示:
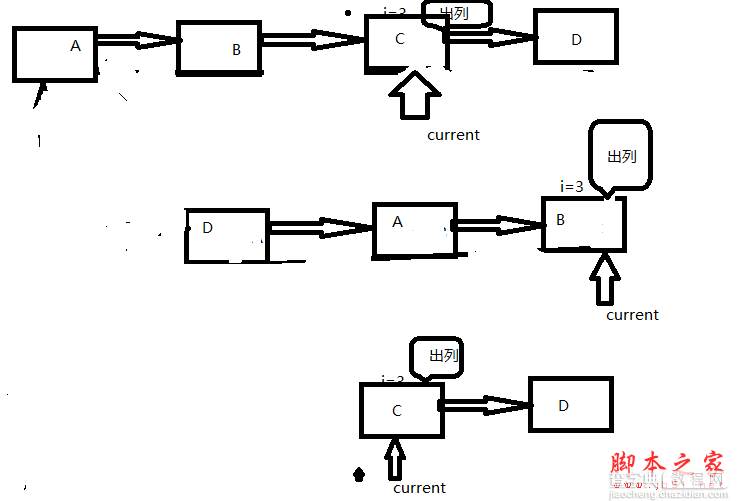
这个算法的时间的复杂度是O(n2)
}
还和大家分享的一个例子,就是我做做一个类似与网易邮箱的产品时候,几千万甚至数以亿级的大数量登录的时候,发现用户登录的时候真他妈的慢,你猜我开始是怎么做的,就是直接查数据库,这当然是不行的。这怎么办了, 最后,我在一个高人的指教下,发现登录的时候速度飞快,怎么搞的。我把所有的数据库的数据读入到内存中,然后把数据用链表把他们串起来,到我查询某个用户时候,只比较用户的 字节数。
这就是我眼中的链表结构。


