题目要求如下:
给定一个数组input[],
如果数组长度n为奇数,则将数组中最大的元素放到output[]数组最中间的位置,
如果数组长度n为偶数,则将数组中最大的元素放到 output[] 数组中间两个位置偏右的那个位置上,
然后再按从大到小的顺序,依次在第一个位置的两边,按照一左一右的顺序,依次存放剩下的数。
这种处理后结果,如果按照元素的值表示一种分布的图形的话,那绘制后的图形应该是正态分布。
关于正态分布:
正态分布(Normal distribution)又名高斯分布(Gaussian distribution),是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。若随机变量X服从一个数学期望为μ、方差为σ^2的高斯分布,记为N(μ,σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。因其曲线呈钟形,因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是μ= 0,σ = 1的正态分布。
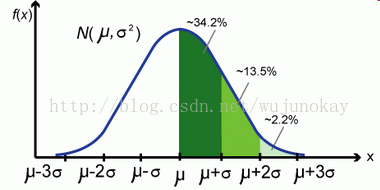
这里只是从结果上产生联系,算法与正态分布无关。
代码实现如下:
void sort(int input[],int output[], int n) { int m=n; //cout<<m<<endl; int i,j,temp; bool exchange;//交换标志 for(i=0;i<m-1;i++) { //最多做n-1趟排序 exchange=FALSE; //本趟排序开始前,交换标志应为假 for(j=m-2;j>=i;j--) //对当前无序区R[i..n]自下向上扫描 if(input[j+1]<input[j]) {//交换记录 temp=input[j+1]; //R[0]不是哨兵,仅做暂存单元 input[j+1]=input[j]; input[j]=temp; exchange=TRUE; //发生了交换,故将交换标志置为真 } if(!exchange) //本趟排序未发生交换,提前终止算法 break; //cout<<input[5]<<endl; } for(int wc1=0; wc1<m; wc1++)//只是来显示排序结果~ { cout<<input[wc1]<<" "; } cout << endl; int q=m-1; if((m%2)==0) { int mid=m/2; for (int tempmid=0; tempmid<=mid; tempmid++)//注意循环语句的执行顺序 { output[mid+tempmid]=input[q]; q--; output[mid-tempmid-1]=input[q]; q--; } } if((m%2)!=0)//注意循环语句的执行顺序 { int mid=q/2; output[mid]=input[q]; for (int tempmid=1;tempmid<=mid;tempmid++) { q--; output[mid-tempmid]=input[q]; q--; output[mid+tempmid]=input[q]; } } for(int wc=0; wc<m; wc++) { cout<<output[wc]<<" "; } cout << endl; }
int main() { int input[] = {3, 6, 1, 9, 7, 8, 2}; int wc=0; int nCount = sizeof(input)/sizeof(int); for(wc=0; wc<nCount; wc++)// { cout<<input[wc] << " "; //cout<<"n"<<endl; } cout << endl; int output[]= {3, 6, 1, 9, 7, 8, 2}; sort(input,output, nCount); return 0; }
测试结果:
当int input[] = {3, 6, 1, 9,7, 8, 2, 10};,结果如下:
3 6 1 9 7 8 2 10
1 2 3 6 7 8 9 10
1 3 7 9 10 8 6 2
当int input[] = {3, 6, 1, 9,7, 8, 2, 10};,结果如下:
3 6 1 9 7 8 2
1 2 3 6 7 8 9
2 6 8 9 7 3


