C语言cos()函数:求余弦值
头文件:
#include <math.h>
cos() 函数用来求余弦值,即求角的临边长度除以斜边长度的比值,其原型为:
double cos(double x);
【参数】x 为一个弧度。
【返回值】返回-1 至1 之间的计算结果。
弧度与角度的关系为:
弧度 = 180 / π 角度
角度 = π / 180 弧度
使用 rtod( ) 函数可以将弧度值转换为角度值。
注意,使用 GCC 编译时请加入-lm。
【实例】求两个角度的余弦值并输出,
#include<stdio.h> #include<math.h> int main(void) { double angl,result; angl = 1; result = cos(angl);/*求余弦值*/ printf("cos(%lf) is %lfn",angl,result);/*格式化输出*/ angl = 3.1415926; result = cos(angl);/*求余弦值*/ printf("cos(%lf) is %lfn",angl,result);/*格式化输出*/ return 0; }
运行结果:
cos(1.000000) is 0.540302 cos(3.141593) is -1.000000
程序中的参数都是直接使用的弧度值,如果只知 道角度,可以使用角度乘以 π / 180 的方法得到弧度值。
C语言cosh()函数:求双曲余玄值
头文件:
#include <math.h>
cosh()用来计算参数x 的双曲余玄值,然后将结果返回。其原型为:
double cosh(double x);
双曲余弦的数学定义式为:
(exp(x)+exp(x))/2
即
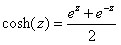
注意,使用 GCC 编译时请加入-lm。
双曲余弦在区间 -5 <= x <= 5 上的函数图像。
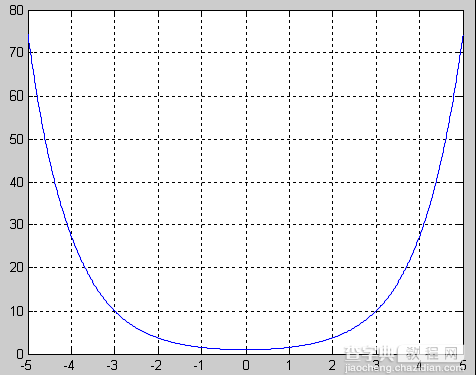
【实例】求0.5的双曲余弦值。
#include <math.h> main(){ double answer = cosh(0.5); printf("cosh(0.5) = %fn", answer); }
运行结果:
cosh(0.5) = 1.127626
又如,求双曲余弦上某一点的值。
#include<stdio.h> #include<math.h> int main(void) { double resut; double x =1; resut = cosh(x);/*求双曲余弦值*/ printf("cosh(%lf) = %lfn",x,resut);/*格式化输出*/ return 0; }
运行结果:
cosh(1.000000) = 1.543081
程序先定义两个double型变量,resut保存计算结果,x提供双曲余弦函数点。语句resut = cosh(x);的作用是求该函数上x点对应的数值,然后把结果赋值给resut。
C语言acos()函数:求反余弦的值
头文件:
#include <math.h>
acos() 函数返回一个以弧度表示的反余弦值,其原型为:
double acos (double x);
【参数】x 为余弦值,范围为 -1 到 1 之间,超出此范围将会导致错误,并设置 errno 的值为 EDOM.
【返回值】返回 0 至 π 之间的计算结果,单位为弧度,在函数库中角度均以弧度来表示。
弧度与角度的关系为:
弧度 = 180 / π 角度
角度 = π / 180 弧度
注意:使用 GCC 编译时请加入-lm。
【实例】求 0.5 的反余弦。
#include <math.h> main(){ double angle; angle = acos(0.5); printf("angle = %fn", angle); }
运行结果:
angle = 1.047198
又如,由余弦值求对应的角度。
#include<stdio.h> #include<math.h> int main(void) { double angl,result; angl = 1; result =acos(cos(angl));/*求反余弦值*/ printf("acos(%lf) is %lfn",cos(angl),result);/*格式化输出*/ angl = 3.1415926; result = acos(cos(angl));/*求反余弦值*/ printf("acos(%lf) is %lfn",cos(angl),result);/*格式化输出*/ return 0; }
运行结果:
acos(0.540302) is 1.000000 acos (-1.000000) is 3.141593
这个例子可以对照余弦函数例子学习,示例中都是使用余弦值作为参数,然后再使用 acos() 函数求出该角度以便对比。


