归并排序算法思想:

分而治之(divide - conquer);每个递归过程涉及三个步骤

第一, 分解: 把待排序的 n 个元素的序列分解成两个子序列, 每个子序列包括 n/2 个元素.

第二, 治理: 对每个子序列分别调用归并排序MergeSort, 进行递归操作

第三, 合并: 合并两个排好序的子序列,生成排序结果.

public static void mergeSort(int[] a, int[] tmp, int left, int right) { if (left < right) { int mid = left + (right - left) / 2; mergeSort(a, tmp, left, mid);// 左排序 mergeSort(a, tmp, mid + 1, right);// 右排序 merge(a, tmp, left, mid + 1, right);// 左右合并 } } public static void merge(int[] a, int[] tmp, int left, int rightPos, int right) { int leftEnd = rightPos - 1; int tmpPos = left; int num = right - left + 1; while (left <= leftEnd && rightPos <= right) { if (a[left] < a[rightPos]) { tmp[tmpPos++] = a[left++]; } else { tmp[tmpPos++] = a[rightPos++]; } } while (left <= leftEnd) { tmp[tmpPos++] = a[left++]; } while (rightPos <= right) { tmp[tmpPos++] = a[rightPos++]; } for (int i = 0; i < num; i++, right--) { a[right] = tmp[right]; } }

归并算法示意图：

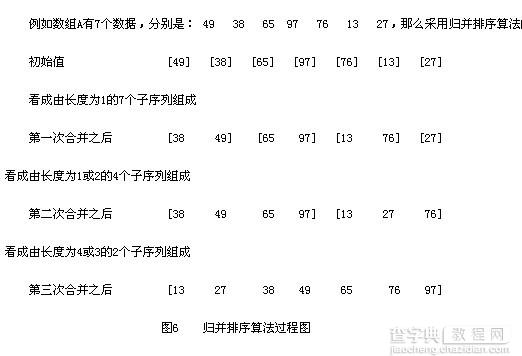
以上所述就是本文的全部内容了，希望大家能够喜欢。