使用几何画板检验几何命题正确性的方法
发布时间:2016-05-05 来源:查字典编辑
摘要:例如:我们知道以任意三角形的三条中线为边,可以构成新的三角形。那么如果以任意三角形的三条角平分线(或高)为边,能否构成新的三角形呢?我们可以...
例如:我们知道以任意三角形的三条中线为边,可以构成新的三角形。那么如果以任意三角形的三条角平分线(或高)为边,能否构成新的三角形呢?
我们可以用几何画板画图进行验证,具体步骤如下:
步骤一 打开几何画板,使用多边形工具任意绘制△ABC,依次选中∠A、∠B、∠C执行“构造”——“角平分线”命令,就得到了如下图所示的△ABC三个内角的角平分线AD、BE、CF。
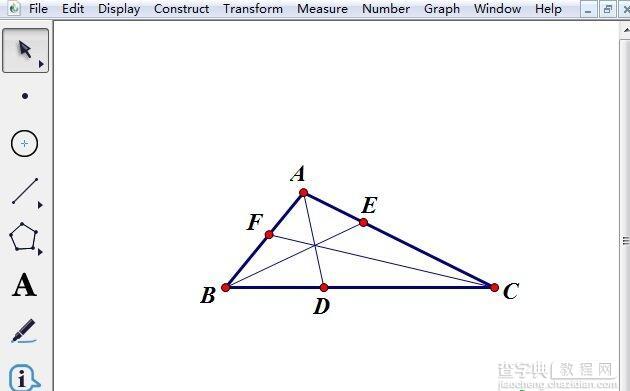 在几何画板中绘制三角形三个内角平分线示例
在几何画板中绘制三角形三个内角平分线示例
步骤二 选择移动箭头工具,选中点B和角平分线CF,执行“构造”——“以圆心和半径画圆”命令,就得到了以点B为圆心,以CF长为半径的圆。
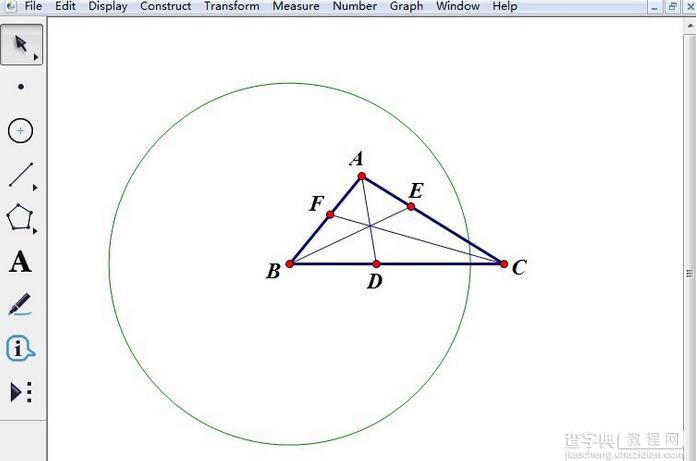 绘制以点B为圆心,CF长为半径的圆示例
绘制以点B为圆心,CF长为半径的圆示例
步骤三 选择移动箭头工具,选中点E和角平分线AD,执行“构造”——“以圆心和半径画圆”命令,就得到了以点E为圆心,AD长为半径画圆。
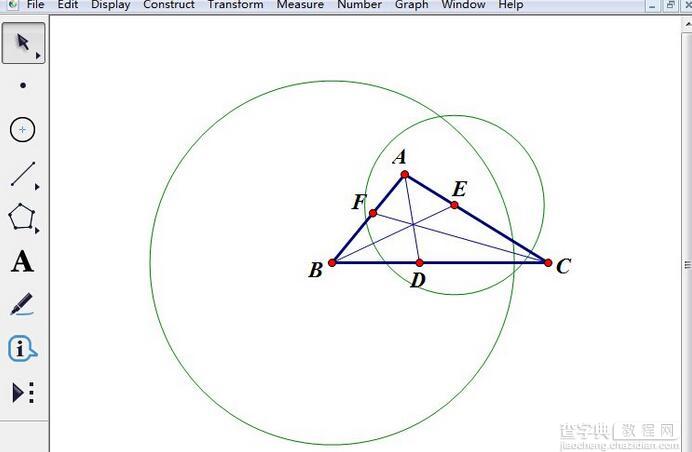 绘制以点E为圆心,AD长为半径的圆示例
绘制以点E为圆心,AD长为半径的圆示例
步骤四 拖动点A,改变△ABC的形状,发现两圆不一定有交点。这说明:以任意三角形的三条角平分线为边,不一定能构成三角形。
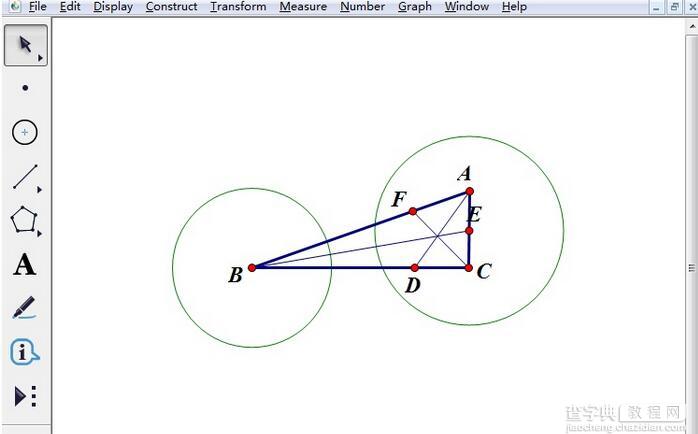 演示两圆无交点验证命题错误示例
演示两圆无交点验证命题错误示例
用类似方法也可以验证以任意三角形的三条高为边,不一定能构成三角形,这里就不多做介绍,大家可以自己动手练习一下。


